Ta có như sau:

\(\dfrac{2}{3}\) số thứ nhất \(=\dfrac{3}{4}\) số thứ hai \(=\dfrac{4}{5}\) số thứ ba tức là

\(\dfrac{12}{18}\) số thứ nhất = \(\dfrac{12}{16}\) số thư hai = \(\dfrac{12}{15}\)số thứ ba, nên

\(\dfrac{1}{18}\) số thứ nhất = \(\dfrac{1}{16}\) số thứ hai = \(\dfrac{1}{15}\) số thứ ba

Coi số thứ nhất là 18 phần bằng nhau thì số thứ hai là 16 phần và số thứ ba là 15 phần như thế

Tổng số phần bằng nhau là

\(18+16+15=49\) (phần)

Giá trị 1 phần là:

\(147:49=3\)

Số thứ nhất là:

\(3\times18=54\)

Số thứ hai là

\(3\times16=48\)

Số thứ ba là

\(3\times15=45\)

2/3 số thứ nhất = 3/4 số thứ hai = 4/5 số thứ ba. Vậy: 

12/18 số thứ nhất = 12/16 số thư hai = 12/15 số thứ ba

=> 1/18 số thứ nhất = 1/16 số thứ hai = 1/15 số thứ ba

Tổng số phần bằng nhau là

18 + 16 +15 = 49 (phần)

Giá trị 1 phần là

147 : 49 = 3

Số thứ nhất là

3 x 18 = 54 (đơn vị)

Số thứ hai là

3 x 16 = 48

Số thứ ba là:

3 x 15 = 45

`@` `\text {Ans}`

`\downarrow`

`-` `3` phân số bằng phân số `4/-12`:

`-1/3; -2/6; -3/9`

3 phân số bằng phân số \(\dfrac{4}{-12}\)

\(\dfrac{5}{-15}\);\(\dfrac{6}{-18}\);\(\dfrac{10}{-30}\)

Vì khi người đó đi xe đạp xuôi gió hết 3 phút, ngược gó hết 4 phút mà đi khi trời lặng gió là lúc không có gió nên:

- Người đó cần 3 phút 30 giây để đi hết 1 km.

Vì khi người đó đi xe đạp xuôi gió hết 3 phút, ngược gó hết 4 phút mà đi khi trời lặng gió là lúc không có gió nên:

- Người đó cần 3 phút 30 giây để đi hết 1 km.

\(\left(x^2+8x\right)+8\left(x^2+8x\right)=48\)

Đặt: \(u=x^2+8x\)

\(\Rightarrow u^2+8u=48\)

\(\Leftrightarrow u^2+8u-48=0\)

\(\Leftrightarrow u^2-4u+12u-48=0\)

\(\Leftrightarrow u\left(u-4\right)+12\left(u-4\right)=0\)

\(\Leftrightarrow\left(u+12\right)\left(u-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}u+12=0\Leftrightarrow u=-12\\u-4=0\Leftrightarrow u=4\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x^2+8x=-12\\x^2+8x=4\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+8x+12=0\\x^2+8x-4=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-4+2\sqrt{5}\\x=-4-2\sqrt{5}\\x=-2\\x=-6\end{matrix}\right.\)

\(\Leftrightarrow x^4+16x^3+64x^2+8x^2+64x=48\\ \Leftrightarrow x^4+16x^3+72x^2+64x-48=0\\ \Leftrightarrow\left(x+2\right)\left(x+6\right)\left(x^2+8x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+2=0\\x+6=0\\x^2+8x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-6\\x=-4\pm2\sqrt{5}\end{matrix}\right.\)

Vậy...

(x+0,3)+(x+0,9)+(x+1,5)+......+(x+5,1)+(x+5,7)=63

(x + x + x + ... + x + x) + (0,3 + 0,9 + 1,5 + ... + 5,1 + 5,7) = 63

Xét tổng 0,3 + 0,9 + 1,5 + ... + 5,1 + 5,7:

Số số hạng của tổng đó là: 

(5,7 - 0,3) : 0,6 + 1 = 10 số

Tổng là: (5,7 + 0,3) x 10 : 2 = 30

Vì tổng có 10 số hạng nên x + x + x + ... + x + x có 10 số 

Ta có:

 \(10\times x+30=63\\ 10\times x=63-30\\ 10\times x=33\\ x=33:10\\ x=3,3\)

Ta thấy: 0,9 = 0,3 x 3; 1,5 = 0,3 x 5,...

Do đó, ta đặt và có: B = 0,3 + 0,9 + ... + 5,7 = 0,3 x (1 + 3 + ... + 19). 

Đặt A = 1 + 3 + ... + 19

Số số hạng trong phép cộng A là: \(\dfrac{19-1}{2}+1=10\) ((số cuối - số đầu) : khoảng cách + 1)

Mỗi x ứng với 1 số hạng nên có 10 số hạng, cũng tức có 10 số x.

Mặt khác, tổng A bằng: \(\dfrac{\left(19+1\right)x10}{2}\) = 100 ((số cuối + số đầu) x số số hạng : 2).

Do đó: B = 0,3 x 100 = 30.

Ta có: (x + 0,3) + (x + 0,9) + ... + (x + 5,7) = 63

          10x + 30 = 63 (do có 10 số x, tổng các số bằng 30)

          10x = 33

              x = 3,3.

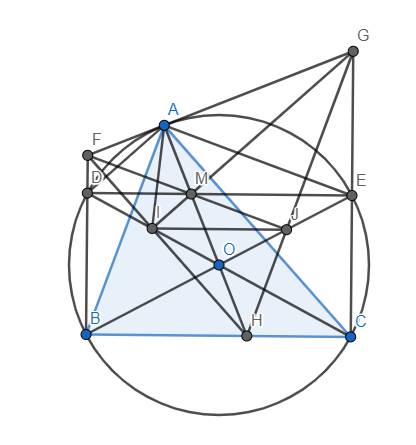
a) Theo đề bài, dễ thấy \(\widehat{FBH}=90^o\). Do FA tiếp xúc (O) tại A nên \(\widehat{FAH}=90^o\). Từ đó suy ra \(\widehat{FBH}=\widehat{FAH}=90^o\), suy ra tứ giác FAHB nội tiếp.

b) Nhận thấy \(\widehat{FAD}=\widehat{FBA}\) vì chúng lần lượt là góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp chắn cung AD. Suy ra \(\Delta FAD~\Delta FBA\left(g.g\right)\) \(\Rightarrow\dfrac{FA}{FB}=\dfrac{FD}{FA}\) \(\Rightarrow FA^2=FB.FD\). Tương tự, ta có \(GA^2=GE.GC\). Cộng theo vế 2 hệ thức vừa tìm được, suy ra đpcm.

c) Ta có \(\widehat{ADI}=\widehat{AEG}=\widehat{ABC}=\widehat{AFH}=\widehat{AFI}\) nên tứ giác AFDI nội tiếp, suy ra \(\widehat{FAD}=\widehat{FID}\). Mà \(\widehat{FID}=\widehat{OIH}\) còn \(\widehat{FAD}=\widehat{FBA}=\widehat{FHA}=\widehat{OHI}\) nên từ đó suy ra \(\widehat{OIH}=\widehat{OHI}\) hay tam giác OHI cân tại O hay \(OI=OH\). Hoàn toàn tương tự, ta có \(OJ=OH\), suy ra đpcm.

d) Ta có \(\widehat{HIC}=\widehat{AHF}=90^o-\widehat{AFH}=90^o-\widehat{ABC}=90^o-\widehat{GAC}\) \(=90^o-\widehat{GHC}=\widehat{HGC}\) nên tứ giác HIGC nội tiếp. Do đó \(\widehat{GIH}=180^o-\widehat{HCG}=90^o\) hay \(GI\perp HF\) tại I. Tương tự, ta có \(FJ\perp HG\) tại J. Mặt khác, \(HA\perp FG\) tại A nên HA, FJ, GI sẽ đồng quy tại trực tâm M của tam giác FGH.

 Ta sẽ chứng minh M di chuyển trên DE (dễ dàng kiểm tra DE cố định). Thật vậy, dễ thấy 5 điểm A, M, I, D, F cùng nằm trên 1 đường tròn, do đó \(\widehat{DMI}=\widehat{DFI}=90^o-\widehat{BHF}\). Tương tự, ta có \(\widehat{JME}=90^o-\widehat{GHC}\). Lại có tứ giác IMJH nội tiếp nên \(\widehat{IMJ}=180^o-\widehat{IHJ}=180^o-\widehat{FHG}\). Từ đây suy ra \(\widehat{DMI}+\widehat{IMJ}+\widehat{JME}=360^o-\left(\widehat{BHF}+\widehat{FHG}+\widehat{GHC}\right)=180^o\), hay D, M, E thẳng hàng, tức là M thuộc DE. Ta có đpcm.

Tổng số học sinh là

\(20+26=46\left(hs\right)\)

Tổng số học sinh thích thi cả hai môn là 

\(46-\left(30-2\right)=18\left(hs\right)\)

\(A=3\left(x+2\sqrt{x}\right)-\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)

\(=3x+6\sqrt{x}-\left(x-1\right)\)

\(=3x+6\sqrt{x}-x+1\)

\(=2x+6\sqrt{x}+1\)

\(B=\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)-2\left(\sqrt{x}-1\right)^2\)

\(=x+3\sqrt{x}+\sqrt{x}+3-2\left(x-2\sqrt{x}+1\right)\)

\(=x+4\sqrt{x}+3-2x+4\sqrt{x}-2\)

\(=-x+8\sqrt{x}+1\)

\(C=3x-3\sqrt{x}-2+\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)

\(=3x-3\sqrt{x}-2+\left(\sqrt{x^2}-1\right)\)

\(=3x-3\sqrt{x}-2+x-1\)

\(=4x-3\sqrt{x}-3\)

\(D=\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)-\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)\)

\(=x-9-\left(2x-3\sqrt{x}-2\right)\)

\(=x-9-2x+3\sqrt{x}+2\)

\(=-x+3\sqrt{x}-7\)

\(E=\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)-2\left(2\sqrt{x}-1\right)\left(\sqrt{x}+2\right)\)

\(=\sqrt{x^2}-2^2-2\left(2x+4\sqrt{x}-\sqrt{x}-2\right)\)

\(=x-4-2\left(2x+3\sqrt{x}-2\right)\)

\(=x-4-4x-6\sqrt{x}+4\)

\(=-3-6\sqrt{x}\)

\(a,DKXD:x\ge0\)

\(b,A=\sqrt{x-\sqrt{x^2-4x+4}}\)

\(=\sqrt{x-\sqrt{\left(x-2\right)^2}}\)

\(=\sqrt{x-\left|x-2\right|}\)

\(=\sqrt{x-\left(x-2\right)}\)

\(=\sqrt{x-x+2}\)

\(=\sqrt{2}\)

\(B=50-3\sqrt{98}+2\sqrt{8}+3\sqrt{32}-5\sqrt{18}\)

\(=50-3.\sqrt{7^2.2}+2\sqrt{2^2.2}+3\sqrt{4^2.2}-5\sqrt{3^2.2}\)

\(=50-3.7\sqrt{2}+2.2\sqrt{2}+3.4\sqrt{2}-5.3\sqrt{2}\)

\(=50-21\sqrt{2}+4\sqrt{2}+12\sqrt{2}-15\sqrt{2}\)

\(=50+\sqrt{2}.\left(-21+4+12-15\right)\)

\(=50+\sqrt{2}.\left(-20\right)\)

\(=50-20\sqrt{2}\)

\(C=\left(\sqrt{3}+\sqrt{5}+\sqrt{7}\right)\left(\sqrt{3}+\sqrt{5}-\sqrt{7}\right)\)

\(=\left(\sqrt{3}+\sqrt{5}\right)^2-\sqrt{7}^2\)

\(=\sqrt{3}^2+2.\sqrt{3}.\sqrt{5}+\sqrt{5}^2-7\)

\(=2\sqrt{15}+3+5-7\)

\(=2\sqrt{15}+1\)

Nghĩ ra xong tính thử thấy đúng định nàm xong thấy mẹ giải r ấy:")). Với nại con còn nhỏ nắm, hong bic nhiều cái mà nớp 9 hay sử dụng nữa ý, sợ dùng sai;-;.