1 cửa hàng có 120 kg đườngvà bán hết trong 3 ngày ngày 1 của hàng bán đc 25% sood đường ngày thứ hai của hàng bán đc 4/9 số đường còn lại.tính số đường bán đc của ngày thứ 3 và ngày thứ 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


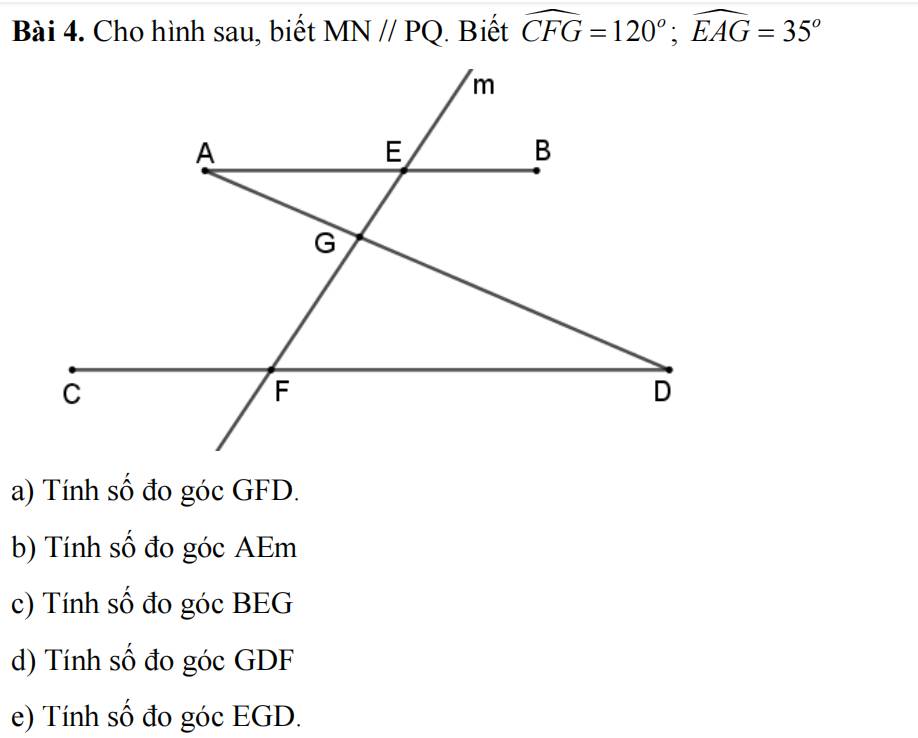
a. Ta có: góc GFD + góc GFC = 180° ( 2 góc kề bù)
=> Góc GFD = 180°-120° =60°
b. Ta có: góc BEm = góc GFD ( 2 góc đồng vị)
=> Góc BEm = 60°
Mà góc BEm + góc AEm =180° ( 2 góc kề bù)
=> 180°-60°=120°
c. Góc BEG = góc AEm (2 góc đối đỉnh) => Góc BEG =120°
d. Ta có: góc GDF = góc EAG ( 2 góc so le trong)
=> Góc GDF = 35°
e. Ta có: góc DGF + góc GFD + góc GDF=180° ( tổng 3 góc trong 1 tam giác) => góc DGF =180°-60°-35°= 85°
Mà góc EGD + góc FGD= 180° (2 góc kề bù)
=> Góc EGD = 180°-85°=95°

Lời giải:
a.
$A=\frac{5-x^2}{x^2+3}=\frac{8-(x^2+3)}{x^2+3}=\frac{8}{x^2+3}-1$
Ta thấy: $x^2+3\geq 3, \forall x\in\mathbb{R}$ nên $\frac{8}{x^2+3}\leq \frac{8}{3}$
$\Rightarrow A\leq \frac{8}{3}-1=\frac{5}{3}$
Vậy gtln của $A$ là $\frac{5}{3}$ khi $x^2=0\Leftrightarrow x=0$
b.
$B=\frac{1}{2}-|2-3x|$
Vì $|2-3x|\geq 0, \forall x\in\mathbb{R}$ nên $B\leq \frac{1}{2}-0=\frac{1}{2}$
Vậy gtln của $B$ là $\frac{1}{2}$ khi $|2-3x|=0\Leftrightarrow x=\frac{2}{3}$
c.
Vì $|2x+4|\geq 0, \forall x\in\mathbb{R}$ nên $C\leq -3-0=-3$
Vậy gtln của $C$ là $-3$ khi $|2x+4|=0\Leftrightarrow x=-2$
d.
$|3,4-x|\geq 0$ với mọi $x\in\mathbb{R}$ nên $D\leq 0,5-0=0,5$
Vậy gtln của $D$ là $0,5$ khi $|3,4-x|=0\Leftrightarrow x=3,4$

1) Áp dụng t/c tổng 3 góc trog 1 tg ta có:
(các góc trog )
Khi đó:
(quan hệ góc và cạnh đối diện)
(quan hệ đường xiên hình chiếu)
2) Có vấn đề.
3) Xét vuông tại H và vuông tại H có:
chung
4) Vì
nên
C/m tương tự câu 3):
Áp dụng tc tổng 3 góc trog 1 tg ta có:

a, để A = \(\dfrac{2}{x+5}\) ϵ Z thì 2 ⋮ x + 5
x + 5 ϵ Ư(2) = { -2; -1; 1; 2)
x ϵ { -7; -6; -4; -3}
b, để B = \(\dfrac{2x-3}{x+1}\) ϵ Z thì 2x - 3 ⋮ x + 1 ⇔ 2(x+1) - 5 ⋮ x + 1
x + 1 ϵ Ư(5) ={ -5; -1; 1; 5)
x ϵ { -6; -2; 0; 4}

Chưa ai giúp em hả??? olm tới rồi em
Gọi số máy đội 1, đội 2, đội 3 lần lượt là : x; y; z
Mỗi ngày mỗi máy của đội 1 làm được : 1 : 4 : x = \(\dfrac{1}{4x}\) (cánh đồng)
Mỗi ngày mỗi máy của đội 2 làm được : 1 : 6 : y = \(\dfrac{1}{6y}\) (cánh đồng)
Mỗi ngày mỗi máy của đội 3 làm được : 1 : 8 : z = \(\dfrac{1}{8z}\) (cánh đồng)
Vì năng suất các máy là nhưu nhau nên :
\(\dfrac{1}{4x}=\dfrac{1}{6y}=\dfrac{1}{8z}\)
4x = 6y = 8z
\(\dfrac{x}{6}=\dfrac{y}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{6}=\dfrac{y}{4}\) = \(\dfrac{x-y}{6-4}\)= \(\dfrac{2}{2}\)= 1
x = 1 x 6 = 6; y = 1 x 4 = 4
tay x = 6 vào 4x = 8z ta có : 4.6 = 8.z ⇒ z = 24: 8 = 3
Kết luận số máy các đội 1; 2; 3 lần lượt là 6 máy; 4 máy ; 3 máy

Gọi \(x\) (giờ) là thời gian để 6 máy bơm bơm nước đầy bể.
Số máy bơm và thời gian chảy đầy bể là hai đại lượng tỉ lệ nghịch nên ta có:
\(\dfrac{3}{6}=\dfrac{x}{2}\) nên \(x=\dfrac{3\cdot2}{6}=1\)
Vậy thời gian để 6 máy bơm chảy đầy bể là 1 giờ.

a)\(\dfrac{4}{5}\)x - \(\dfrac{15}{4}\)=\(\left(\dfrac{-1}{2}\right)^2\)
\(\dfrac{16x}{20}\) - \(\dfrac{75}{20}\)=\(\dfrac{1}{4}\)
\(\dfrac{16x-75}{20}\)=\(\dfrac{1}{4}\)
⇒4(16x-75)=20
16x-75=5
16x=80
x=5
b)1 công nhân làm xong công việc trong số ngày:
35x168=5880 (ngày)
28 công nhân làm xong công việc trong số ngày:
5880 : 28 =210 (ngày)
c\(\left(5x-1\right)^4\)=\(\left(5x-6\right)^6\)
\(\left(5x-6\right)^6\) - \(\left(5x-1\right)^4\) =0
\(\left(5x-1\right)^4\) (\(\left(5x-1\right)^2\)-1)=0
⇒5x-1=0⇒5x=1⇒x=\(\dfrac{1}{5}\)
hoặc\(\left(5x-1\right)^2\)-1=0
\(\left(5x-1\right)^2\)=1
⇒5x-1=1 hoặc -1
TH1 5x-1=1 TH2 5x-1=-1
5x=2 5x=0
x=\(\dfrac{2}{5}\) x=0

Số đường bán được trong ngày thứ nhất là:
120 x 25 : 100 = 30 (kg)
Số đường bán được trong ngày thứ hai là :
( 120 - 30) x \(\dfrac{4}{9}\) = 40 (kg)
Số đường bán được trong ngày thứ 3 là :
120 - 30 - 40 = 50 (kg)
đáp số : .....