\(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\)

\(=\sqrt{\sqrt{3^2}+2\sqrt{3}.\sqrt{2}+\sqrt{2^2}}-\sqrt{\sqrt{3^2}-2.\sqrt{3}.\sqrt{2}+\sqrt{2^2}}\)

\(=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\)

\(=\left|\sqrt{3}+\sqrt{2}\right|-\left|\sqrt{3}-\sqrt{2}\right|\)

\(=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\)

\(=2\sqrt{2}\)

`@` `\text {Ans}`

`\downarrow`

`a)`

`A = {x \in N` `|` `x*2=5}`

`x*2 = 5`

`=> x=5 \div 2`

`=> x=2,5`

Vậy, số phần tử của tập hợp A là 1 (pt 2,

`b)`

`B = {x \in N` `|` `x+4=9}`

`x+4=9`

`=> x=9-4`

`=> x=5`

`=>` phần tử của tập hợp B là 5

Vậy, số phần tử của tập hợp B là 1.

`c)`

`C = {x \in N` `|` `2<x \le 100}`

Số phần tử của tập hợp C là:

`(100 - 2) \div 2 + 1 = 50 (\text {phần tử})`

Vậy, tập hợp C gồm `50` phần tử.

giúp mình với, mình đang vội

10800 m² = 1080000 dm² = 108000000 cm²

1 giờ ô tô và xe máy đi được là:

40 + 60 = 100 (km)

Thời gian để 2 xe gặp nhau là:

200 : 100 = 2 (giờ)

Đ/S: 2 giờ

CHÚC EM HỌC TỐT NHα!

a. Độ dài quãng đường từ cảng Sa Kỳ đến đảo lý sơn:

\(2\times15=30\left(km\right)\)

b) Vận tốc của thuyển khi nước lặng:

\(15+2,5=17,5\left(km/h\right)\)

Vận tốc của thuyền khi đi xuôi dòng:

\(17,5+2,5=20\left(km/h\right)\)

Thời gian thuyền đi khi đi xuôi dòng:

\(30:20=1,5\left(h\right)\)

Vậy thời gian thuyền đi xuôi dòng là 1 giờ 30 phút

bạn ơi câu b vtốc của thuyền xuôi dòng là 17,5+2,5 chứ

a, A = \(\dfrac{2022.2023-1}{2022.2023}\) = \(\dfrac{2022.2023}{2022.2023}\) - \(\dfrac{1}{2022.2023}\) = 1 - \(\dfrac{1}{2022.2023}\)

B = \(\dfrac{2021.2022-1}{2021.2022}\) =  \(\dfrac{2021.2022}{2021.2022}\)  - \(\dfrac{1}{2021.2022}\) = 1 - \(\dfrac{1}{2021.2022}\) 

Vì \(\dfrac{1}{2022.2023}\) < \(\dfrac{1}{2021.2022}\)

Nên A > B

b, C = \(\dfrac{2022.2023}{2022.2023+1}\)  

    C = \(\dfrac{2022.2023+1-1}{2022.2023+1}\) = \(\dfrac{2022.2023+1}{2022.2023+1}\) - \(\dfrac{1}{2022.2023+1}\) 

     C = 1  - \(\dfrac{1}{2022.2023+1}\)

     D = \(\dfrac{2023.2024}{2023.2024+1}\) = \(\dfrac{2023.2024+1-1}{2023.2024+1}\) 

     D = 1 - \(\dfrac{1}{2023.2024+1}\)

Vì \(\dfrac{1}{2022.2023+1}\) > \(\dfrac{1}{2023.2024+1}\)

Nên C < D 

Lời giải:

$7(x+9)-3(5-x)=98$

$\Leftrightarrow 7x+63-15+3x=98$

$\Leftrightarrow 10x+48=98$

$\Leftrightarrow 10x=50$

$\Leftrightarrow x=5$

\(7\times\left(x+9\right)-3\times\left(5-x\right)=98\)

\(7x+63-15+3x=98\)

\(10x+48=98\)

\(10x=98-48\)

\(10x=50\)

\(x=5\)

Vậy: \(x=5\)

Đề thiếu. Bạn xem lại.

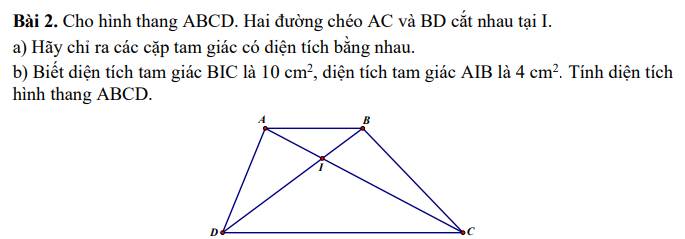
a/ 

Hai tg ABD và tg ABC có chung AB, đường cao từ D->AB = đường cao từ C->AB nên \(S_{ABD}=S_{ABC}\)

Hai tg trên có phần diện tích chung là \(S_{ABI}\Rightarrow S_{ADI}=S_{BCI}\)

Tương tự \(S_{ADC}=S_{BCD}\)

b/

Hai tg AIB và tg BIC có chung BI nên

\(\dfrac{S_{AIB}}{S_{BIC}}=\) đường cao từ A->BD = đường cao từ C-> BD \(=\dfrac{4}{10}=\dfrac{2}{5}\)

Ta có

\(S_{ABD}=S_{ABC}=S_{AIB}+S_{BIC}=4+10=14cm^2\)

Hai tg ABD và tg BCD có chung BD nên

\(\dfrac{S_{ABD}}{S_{BCD}}=\) đường cao từ A->BD = đường cao từ C-> BD\(=\dfrac{2}{5}\)

\(\Rightarrow S_{BCD}=\dfrac{5xS_{ABD}}{2}=\dfrac{5x14}{2}=35cm^2\)

\(S_{ABCD}=S_{ABD}+S_{BCD}=14+35=49cm^2\)

 Vì ^{\(a^2,b^2,c^2\ge0\) nên \(a^2+b^2+c^2\ge0\)}. ĐTXR \(\Leftrightarrow a=b=c=0\), thỏa mãn đk đề bài. Vậy GTNN của \(a^2+b^2+c^2\) là 0, xảy ra khi \(a=b=c=0\)