Cái bạn viết chưa phải 1 phương trình nhé. Bạn xem lại.

a sẽ sử dụng phương pháp chia để trị để giải quyết bài toán này. Ta bắt đầu bằng cách chia các vật thành hai nhóm có số lượng gần bằng nhau.

• Nhóm 1: Các vật có khối lượng từ 1 đến 50 gam.
• Nhóm 2: Các vật có khối lượng từ 51 đến 100 gam.

Để cân các vật trong nhóm 1, ta cần sử dụng một quả cân. Để cân các vật trong nhóm 2, ta cũng cần sử dụng một quả cân.

Vậy, ta cần ít nhất 2 quả cân để cân tất cả các vật có khối lượng là một số tự nhiên từ 1 gam đến 100 gam.

Lời giải:

Gọi tuổi anh và tuổi em hiện nay là $3a$ và $a$ (tuổi) 

6 năm nữa tuổi anh là: $3a+6$ 

6 năm nữa tuổi em là: $a+6$

Theo bài ra ta có: $3a+6=2(a+6)$

$\Rightarrow a=6$ (tuổi) 

Vậy tuổi em hiện nay là 6 tuổi. Tuổi anh hiện nay là $6.3=18$ tuổi.

Số sách ở thư viện thứ nhất:

\(\left(15000+3000\right):2=9000\) (cuốn sách)

Số sách ở thư viện thứ hai:

\(15000-9000=6000\) (cuốn sách)

Đáp số:....

Lời giải:

$\frac{3}{2}B=\frac{3\sqrt{x}}{x+\sqrt{x}+1}$
$\Rightarrow 1-\frac{3}{2}B=1-\frac{3\sqrt{x}}{x+\sqrt{x}+1}=\frac{x-2\sqrt{x}+1}{x+\sqrt{x}+1}=\frac{(\sqrt{x}-1)^2}{x+\sqrt{x}+1}\geq 0$ với mọi $x\geq 0$

$\Rightarrow \frac{3}{2}B\leq 1$

$\Rightarrow B\leq \frac{2}{3}$

Vậy $B_{\max}=\frac{2}{3}$ khi $\sqrt{x}-1=0\Leftrightarrow x=1$

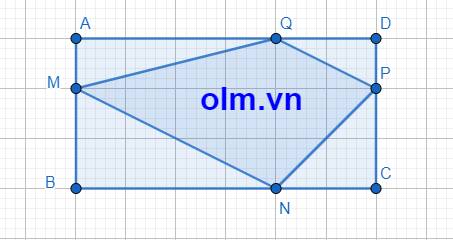
S_AMQ  = \(\dfrac{1}{3}\)S_ABQ (vì hai tam giác có chung chiều cao hạ từ đỉnh Q xuống đáy AB và AM = \(\dfrac{1}{3}\)ABQ)

AQ     =  DA - QD = DA  - \(\dfrac{1}{3}\)DA = \(\dfrac{2}{3}\)DA

S_ABQ =  \(\dfrac{2}{3}\)S_ABD (vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AD và QA = \(\dfrac{2}{3}\)DA)

S_ABD = \(\dfrac{1}{2}\) S_ABCD (vì ABCD là hình chữ nhật) 

S_AMQ = \(\dfrac{1}{3}\)\(\times\)\(\dfrac{2}{3}\)\(\times\)\(\dfrac{1}{2}\) \(\times\) S_ABCD = 162 \(\times\) \(\dfrac{1}{9}\) = 18 (cm²)

S_BMN = \(\dfrac{2}{3}\)S_BCM (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{2}{3}\)BC)

BM = AB - AM = AB - \(\dfrac{1}{3}\)AB = \(\dfrac{2}{3}\)AB 

S_BCM = \(\dfrac{2}{3}\)S_ABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM = \(\dfrac{2}{3}\)AB)

S_ABC = \(\dfrac{1}{2}\)S_ABCD ( vì ABCD là hình chữ nhật)

S_BMN = \(\dfrac{2}{3}\times\dfrac{2}{3}\) \(\times\) \(\dfrac{1}{2}\)S_ABCD = 162 \(\times\) \(\dfrac{2}{9}\) = 36 (cm²)

CN = BC - BN = BC - \(\dfrac{2}{3}\)BC = \(\dfrac{1}{3}\)BC 

S_PCN = \(\dfrac{1}{3}\)S_BPC( vì hai tam giác có cùng chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{1}{3}\)BC 

S_PBC = \(\dfrac{2}{3}\)S_BCD (vì hai tam giác có cùng chiều cao hạ từ đỉnh B xuống đáy CD và CP = \(\dfrac{2}{3}\)CD)

S_BCD = \(\dfrac{1}{2}\)S_ABCD ( vì ABCD là hình chữ nhật)

S_PCN = \(\dfrac{1}{3}\times\dfrac{2}{3}\times\dfrac{1}{2}\)S_ABCD = 162\(\times\)\(\dfrac{1}{9}\) = 18(cm²)

DP = DC - CP = DC - \(\dfrac{2}{3}\)DC = \(\dfrac{1}{3}\)DC 

S_DPQ = \(\dfrac{1}{3}\)S_DCQ (vì hai tam giác có chung chiều cao hạ từ đỉnh Q xuống đáy DC và DP = \(\dfrac{1}{3}\)DC)

S_DCQ = \(\dfrac{1}{3}\)S_ACD (vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AD và DQ = \(\dfrac{1}{3}\)AD)

S_ADC = \(\dfrac{1}{2}\)S_ABCD ( vì ABCD là hình chữ  nhật)

S_DPQ  = \(\dfrac{1}{3}\times\dfrac{1}{3}\times\dfrac{1}{2}\)S_ABCD = 162 \(\times\) \(\dfrac{1}{18}\) = 9 (cm²)

S_MNPQ = S_ABCD - (S_DPQ  + S_PCN + S_BMN + S_AQM)

S_MNPQ = 162 - (9 + 18 + 36 + 18) = 81 (cm²)

Đáp số : 81 cm²

Số viên bi Bình có là:

 $15\times 2=30$  \(viên bi)

Tổng số viên bi của Bình và An là:

 (viên bi)

Trung bình cộng số viên bi của 3 bạn là:

$\left(45+3\right):2=24$ (viên bi) 

Số viên bi của Thịnh là:

$24+3=27$ (viên bi)

Đáp số: ...

1. a) Ta có:

   • Diện tích tam giác ABC là S = 1/2 * AB * AC = 1/2 * 3cm * 4cm = 6cm^2.
   • Vì AD là đường cao của tam giác ABC nên diện tích tam giác ABC cũng bằng 1/2 * AB * CD, tức là: S = 1/2 * AB * CD = 3CD.
     Từ đó suy ra: CD = 2cm.

   b) Gọi E là hình chiếu vuông góc của D trên BC. Ta có:

   • Tam giác ADE và tam giác ABC đồng dạng với tỉ số đồng dạng AD/AB.

   • Tam giác BDE và tam giác ABC đồng dạng với tỉ số đồng dạng AD/AC.
     Do đó, ta có:

   • AI/AB = DE/BC (vì tam giác ADE và tam giác ABC đồng dạng)

   • DE = AD - AE = AD - CD = AD - 2 (vì tam giác ADE vuông tại E và CD là hình chiếu của AD trên BC)

   • BC = AB + AC = 3 + 4 = 7
     Từ đó suy ra: AI/AB = (AD - 2)/7

   Vậy, ta có: AI*AB = (AD - 2)AB/7 = ADAB/7 - 2AB/7 = AD^2/3 - 2/7.

   c) Gọi F là hình chiếu vuông góc của D trên AB. Ta có:

   • Tam giác ADF và tam giác ABC đồng dạng với tỉ số đồng dạng AD/AB.

   • Tam giác CDF và tam giác ABC đồng dạng với tỉ số đồng dạng CD/AC.
     Do đó, ta có:

   • AI/AB = DF/AF (vì tam giác ADF và tam giác ABC đồng dạng)

   • AK/AC = CF/AF (vì tam giác CDF và tam giác ABC đồng dạng)

   • DF + CF = CD = 2

   • AF = AB - BF = AB - AK = 3 - AK (vì BF là hình chiếu của B trên AC và AK là hình chiếu của D trên AC)

   Từ đó suy ra: AI/AB = DF/(DF + CF) = DF/2 = (AD^2 - AF^2)/(2AD^2) = (AD^2 - (AB - AK)^2)/(2AD^2) = (2AK*AC - AK^2)/(2AD^2) = AK/AD - AK^2/(2AD^2).

   Từ b) và c), ta có: AIAB = AD^2/3 - 2/7 = AKAC*(1 - AK^2/(2AD^2)).

   d) Gọi H là hình chiếu vuông góc của I trên BC. Ta có:

   • Tam giác ADH và tam giác ABC đồng dạng với tỉ số đồng dạng AD/AB.

   • Tam giác IDH và tam giác ABC đồng dạng với tỉ số đồng dạng AI/AC.
     Do đó, ta có:

   • ID/AI = DH/AB (vì tam giác IDH và tam giác ABC đồng dạng)

   • DH = CD - CH = 2 - CI (vì tam giác ADH vuông tại H và CI là hình chiếu của I trên BC)

   • AB = 3, AC = 4, BC = 7

   Từ đó suy ra: ID/AI = (CD - CH)/AB = (2 - CI)/3.

   Do đó, ta có: ID/AI = (2 - CI)/3 = (2 - AK)/4 (vì AIAB = AKAC từ c))

   Từ đó suy ra: ID = (2AI - 3AK)/4.

   Vậy, ta có: ID/AI = (2AI - 3AK)/(4AI) = 1 - 3AK/(2AI) = 1 - DH

   18:22
2.  

Số viên bi Bình có là:

 \(15\times2=30\)  \(viên bi)

Tổng số viên bi của Bình và An là:

 (viên bi)

Trung bình cộng số viên bi của 3 bạn là:

\(\left(45+3\right):2=24\) (viên bi) 

Số viên bi của Thịnh là:

\(24+3=27\) (viên bi)

Đáp số: ...

Ta có thể viết lại biểu thức trên dưới dạng:
(6 x 8 -😎 + (8 x 10 -😎 + (10 x 12 -😎 + … + (98 x 100 -😎
= 8 x (6 + 8 + 10 + … + 98) - 8 x 49
= 8 x (6 + 98) x 47 - 8 x 49
= 8 x 104 x 47 - 8 x 49
= 8 x (104 x 47 - 49)
= 8 x 4863
= 38,904

Vậy kết quả của biểu thức là 38,904.