Tìm x biết |x| + |x+3|=5x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Làm xong nhớ tick cho mình đấy nhé !
a) Xét ∆ABM và ∆ACM, ta có :
AB = AC (vì ∆ABC cân tại A)
AM là cạnh chung
MB = MC (vì M là trung điểm của BC)
ð ∆ABM = ∆ACM (c.c.c)
b) Xét ∆AMH và ∆AMK, ta có :
Góc HAM = góc KAM
AM là cạnh chung
Góc AHM = góc AKM
ð ∆AMH = ∆AMK
ð MH = MK (g.c.g)
c) Trong ∆AJI, ta có :
Góc AJI = (180° - góc A) : 2 (1)
Trong ∆ABC, ta có :
Góc abc = (180° - góc A) : 2 (2)
Từ (1) và (2) => góc AJI = góc ABC
Mà 2 góc này ở vị trí đồng vị
ð IJ // BC

Ta có x/2 = 1/6 + 3/y ⇒ x/2 - 1/6 = 3/y ⇒ 3x - 1/ 6 = 3/y
Vậy y( 3x - 1 ) = 18
Mà x; y nguyên nên 3x - 1 nguyên và y; 3x - 1 ϵ Ư( 18 ) = { -1; 1; 2; -2; -3; 3; -6; 6; 18; -18 }
Vì 3x - 1 chia 3 dư 2 nên ( 3x - 1 ) ϵ { 2; -1 }
Nếu 3x - 1 = 2 ⇒ x = 1; y = 9
Nếu 3x - 1 = -1 ⇒ x = 0; y = -18
Vậy các cặp số nguyên ( x; y ) cần tìm là ( 1; 9 ) ; ( 0; -18 )

\(\dfrac{y+z+1}{x}=\dfrac{x+z+2}{y}=\dfrac{x+y-3}{z}\)
\(=\dfrac{\left(y+z+1\right)+\left(x+z+2\right)+\left(x+y-3\right)}{x+y+z}\)
\(=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)
Từ đó suy ra
\(\dfrac{1}{x+y+z}=2\Leftrightarrow x+y+z=\dfrac{1}{2}\).
\(\left\{{}\begin{matrix}y+z+1=2x\\x+z+2=2y\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{5}{6}\\z=-\dfrac{5}{6}\end{matrix}\right.\).

\(\left(\left|x\right|-2011\right)^{\left(2+2008\right)}\cdot\left(2+2009\right)=-\left(2^3-3^2\right)^{2009}\)
\(\left(\left|x\right|-2011\right)^{2010}\cdot2011=-\left(8-9\right)^{2009}\)
\(\left(\left|x\right|-2011\right)^{2010}\cdot2011=-\left(-1\right)^{2009}\)
\(\left(\left|x\right|-2011\right)^{2010}\cdot2011=-\left(-1\right)\)
\(\left(\left|x\right|-2011\right)^{2010}\cdot2011=1\)
\(\left(\left|x\right|-2011\right)^{2010}=\dfrac{1}{2011}\)
???

2012 . | x - 2011| + (x-2011)2 = 2013 . | 2011 - x|
|x-2011|.|x-2011| + 2012 . | x - 2011| - 2013 . | 2011- x| =0
|x - 2011|.| x - 2011| + 2012 .| x - 2011| - 2013 | x - 2011| = 0
| x- 2011| .| x -2011| - | x - 2011| = 0
| x - 2011|. { | x - 2011| - 1} = 0
\(\left[{}\begin{matrix}\left|x-2011\right|=0\\\left|x-2011\right|-1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=2011\\x=2012\\x=2010\end{matrix}\right.\)
Kết luận x \(\in\) { 2010; 2011; 2012}

Lời giải:
Để $A$ nguyên thì $2x-3\vdots x+1$
$\Rightarrow 2(x+1)-5\vdots x+1$
$\Rightarrow 5\vdots x+1$
$\Rightarrow x+1\in \left\{1; -1; 5; -5\right\}$
$\Rightarrow x\in\left\{0; -2; 4; -6\right\}$

Định lý Pythagoras là mối liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông. Định lý phát biểu rằng bình phương cạnh huyền bằng tổng bình phương của hai cạnh còn lại.

b) \(\left(x-1\right)^3=\dfrac{1}{8}\)
\(\left(x-1\right)^3=\left(\dfrac{1}{2}\right)^3\)
\(x-1=\dfrac{1}{2}\)
\(x=\dfrac{1}{2}+1\)
\(x=\dfrac{3}{2}\)
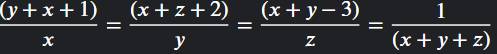
Trong bài này chỉ có 3 trường hợp.
TH1: \(x< -3\).
TH2: \(-3\le x< 0\).
TH3; \(x\ge0\).