(-0, 1) +0, 2+(-0, 3) +0, 4 - 0, 5+0, 6-0, 7 -(-0, 8)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2\(x\)( 0,5 + \(\dfrac{2}{3}\)) : \(\dfrac{7}{3}\) = 0,25
2\(x\)( \(\dfrac{1}{2}\) + \(\dfrac{2}{3}\)) = 0,25 \(\times\) \(\dfrac{7}{3}\)
2\(x\) \(\times\) \(\dfrac{7}{6}\) = \(\dfrac{7}{12}\)
2\(x\) = \(\dfrac{7}{12}\) : \(\dfrac{7}{6}\)
2\(x\) = \(\dfrac{1}{2}\)
\(x\) = \(\dfrac{1}{2}\):2
\(x\) = \(\dfrac{1}{4}\)

b, B = \(\dfrac{1}{2}\) - \(\dfrac{1}{2^2}\) + \(\dfrac{1}{2^3}\) - \(\dfrac{1}{2^4}\)+.....+ \(\dfrac{1}{2^{99}}\) - \(\dfrac{1}{2^{100}}\)
2 \(\times\) B = 1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{2^2}\) - \(\dfrac{1}{2^3}\) + \(\dfrac{1}{2^4}\)-.......-\(\dfrac{1}{2^{99}}\)
2 \(\times\) B + B = 1 - \(\dfrac{1}{2^{100}}\)
3B = ( 1 - \(\dfrac{1}{2^{100}}\))
B = ( 1 - \(\dfrac{1}{2^{100}}\)) : 3
A = 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\)+ \(\dfrac{1}{3^3}\)+......+ \(\dfrac{1}{3^{n-1}}\) + \(\dfrac{1}{3^n}\)
A\(\times\) 3 = 3 + 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^2}\)+....+ \(\dfrac{1}{3^{n-1}}\)
A \(\times\) 3 - A = 3 - \(\dfrac{1}{3^n}\)
2A = 3 - \(\dfrac{1}{3^n}\)
A = ( 3 - \(\dfrac{1}{3^n}\)) : 2

`x/5-2/3(x-6)=(-3)/10`
`=>x/5-2/3x+4=-3/10`
`=>1/5x-2/3x=-3/10-4`
`=>3/15x-10/15x=-3/10-40/10`
`=>-7/15x=-43/10`
`=>x=-43/10:(-7)/15`
`=>x=-43/10*15/(-7)`
`=>x=129/14`

a)
`(1/2+2x)(2x-3)=0`
\(=>\left[{}\begin{matrix}\dfrac{1}{2}+2x=0\\2x-3=0\end{matrix}\right.\\ =>\left[{}\begin{matrix}2x=-\dfrac{1}{2}\\2x=3\end{matrix}\right.\\ =>\left[{}\begin{matrix}x=-\dfrac{1}{4}\\x=\dfrac{3}{2}\end{matrix}\right.\)
b)
`1/4-(2x+1/2)^2=0`
`=>(2x+1/2)^2=1/4`
\(=>\left[{}\begin{matrix}2x+\dfrac{1}{2}=\dfrac{1}{2}\\2x+\dfrac{1}{2}=-\dfrac{1}{2}\end{matrix}\right.\\ =>\left[{}\begin{matrix}2x=0\\2x=-1\end{matrix}\right.\\ =>\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)

/////////////////////////////////////////////////////////////////////////'
1/2^2+1/3^2+.....+1/2010^2
ko tính đc nhưng có thể xét lớn hơn hoặc nhỏ hơn bao nhiêu

\(A=\dfrac{10^{2004}+1}{10^{2003}+1}>\dfrac{10^{2004}+1+9}{10^{2003}+1+9}=\dfrac{10^{2004}+10}{10^{2003}+10}.\\ =\dfrac{10\left(10^{2003}+1\right)}{10\left(10^{2002}+1\right)}=\dfrac{10^{2003}+1}{10^{2002}+1}=B.\\ \Rightarrow A>B.\)

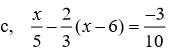
A =(-0,1) + 0,2 + (-0,3) + 0,4 - 0,5 + 0,6 - 0,7 - (-0,8)
B = -0,1 + 0,2 - 0,3 + 0,4 - 0,5 + 0,6 - 0,7 + 0,8
B = -0,1 + ( 0,2 + 0,8) - ( 0,3 + 0,7) + ( 0,6 + 0,4) - 0,5
B = -0,1 + 1 - 1 + 1 - 0,5
B = - ( 0,1 + 0,5) + ( 1 - 1) + 1
B = -0,6 + 0 + 1
B = 0,4