Câu 2: Một người có 4 cái quần khác nhau, 6 cái áo khác nhau, 3 chiếc cà vạt khác nhau. Để chọn một cái quần hoặc một cái áo hoặc một cái cà vạt thì số cách chọn khác nhau là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y=\frac{\frac{1-\cos4x}{2}+3\sin4x}{\cos4x-\sin4x+3}=\frac{6\sin4x-\cos4x+1}{2\cos4x-2\sin4x+6}\)
\(\Leftrightarrow\left(2y+1\right)\cos4x-\left(2y+6\right)\sin4x=1-6y\)(*)
(*) có nghiệm khi và chỉ khi: \(\left(2y+1\right)^2+\left(2y+6\right)^2\ge\left(1-6y\right)^2\)
\(\Leftrightarrow-7y^2+10y+9\ge0\Leftrightarrow\frac{5-2\sqrt{22}}{7}\le y\le\frac{5+2\sqrt{22}}{7}\)

Lời giải
Áp dụng BĐT (ac+bd)2≤(c2+d2)(a2+b2) .
Đẳng thức xảy ra khi ac=bd .
Ta có: (3sinx+4cosx)2≤(32+42)(sin2x+cos2x)=25
⇒–5≤3sinx+4cosx≤5⇒–4≤y≤6 .
Vậy maxy=6 , đạt được khi tanx=34 .
miny=–4 , đạt được khi tanx=–34 .
Dùng \(asinx+b.cosx=c\) cũng được :
C 2 : \(y-1=3sinx+4cosx\) ( * )
( * ) có no \(\Leftrightarrow3^2+4^2\ge\left(y-1\right)^2\Leftrightarrow\left(y-1\right)^2\le25\)
\(\Leftrightarrow-5\le y-1\le5\)
\(\Leftrightarrow-4\le y\le6\)
Xét Min \(y=-4\) ; ta có : \(3sinx+4cosx+1=-4\)
\(\Leftrightarrow3sinx+4cosx=-5\)
Đến đây ; xét cos x = 0 hoặc cos x khác 0 ; rồi chia cho cos^2 x ; tìm được x ( bn tự làm )
Xét Max \(y=6\) ; làm tương tự như trên

\(\sin3x+\sqrt{3}\cos3x=2\sin2x\)
<=> \(\frac{1}{2}.sin3x+\frac{\sqrt{3}}{2}.cos3x=sin2x\)
<=> \(sin\left(3x+\frac{\pi}{3}\right)=sin2x\)
<=> \(\orbr{\begin{cases}3x+\frac{\pi}{3}=2x+k2\pi\\3x+\frac{\pi}{3}=\pi-2x+k2\pi\end{cases}}\) \(k\inℤ\)
<=> \(\orbr{\begin{cases}x=-\frac{\pi}{3}+k2\pi\\x=\frac{2\pi}{15}+\frac{k2\pi}{5}\end{cases}}\)

sin(2x-40º) = 1 ⇔ 2x-40º = 90º + k360º ⇔ x = 65º + k180º
-180º < x < 180º ⇒ x=65º (k=0),x= -115º (k= -1) .
=>B

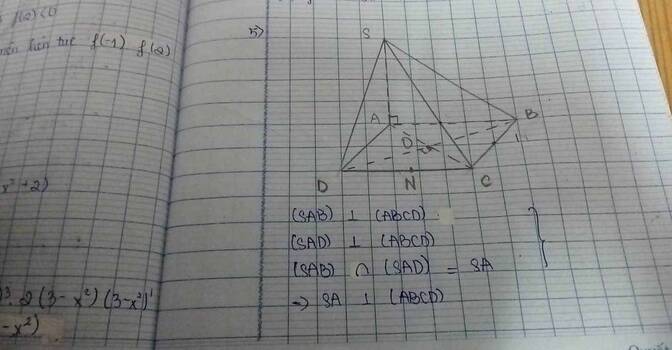
a) (SAB) và (SAD) cùng vuông góc (ABCD), (SAB) và (SAB) có giao tuyến SA => SA vuông góc (ABCD)
=> BC vuông góc SA. Mà BC vuông góc AB nên BC vuông góc (SAB).
Ta cũng có BD vuông góc AS, BD vuông góc AC vì ABCD là hình vuông
=> BD vuông góc (SAC) hay (SAC) vuông góc (SBD).
b) Gọi M là trung điểm của AB, CM cắt AD tại P, H thuộc CM sao cho AH vuông góc CM, K thuộc SH sao cho AK vuông góc SH.
Dễ thấy AN || CM => AN || (SCM) => d(AN,SC) = d(AN,SCM) = d(A,SCM) = d(A,SMP)
Ta có AH vuông góc MP, MP vuông góc AS => MP vuông góc (HAS) => (SMP) vuông góc (HAS)
Vì (SMP) và (HAS) có giao tuyến SH, AK vuông góc SH tại K nên d(A,SMP) = AK
Theo hệ thức lượng thì: \(\frac{1}{AK^2}=\frac{1}{AS^2}+\frac{1}{AM^2}+\frac{1}{AP^2}\)
\(\Rightarrow d\left(AN,SC\right)=d\left(A,SMP\right)=AK=\frac{AS.AM.AP}{\sqrt{AS^2AM^2+AM^2AP^2+AP^2AS^2}}\)
\(=\frac{a\sqrt{2}.\frac{a}{2}.a}{\sqrt{2a^2.\frac{a^2}{4}+\frac{a^2}{4}.a^2+a^2.2a^2}}=\frac{a\sqrt{22}}{11}.\)


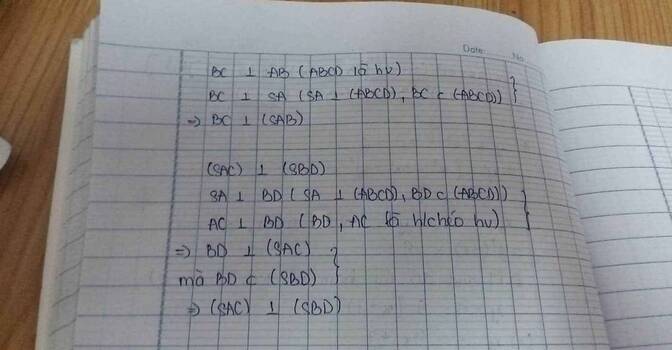

Để chọn ra một cái quần hoặc một csai áo hoặc một cái cà vạt thì số cách khác nhau là:
\(C^1_4.C^1_6.C^1_3=4.6.3=72\)(cách)
13 cách