\(25\times38=950\)

950

Tổng số tuổi `10` cầu thủ và `1` thủ môn là :

      \(23\times11=253\) (tuổi)

Tổng số tuổi `10` cầu thủ là :

       \(22\times10=220\) (tuổi)

Số tuổi thủ môn là :

      `253-220=33` (tuổi)

Tổng số tuổi 10 cầu thủ và 1 cầu thủ môn là

23 x 11 = 253(tuổi

Tổng số tuổi 10 cầu thủ

22 x 10= 220(tuổi

Số tuổi thủ môn là

253-220=33(tuổi)

Đ/S:33 tuổi 

3\(x\) - 28  = \(x\) + 36

3\(x\) - \(x\)    = 36 + 28

2\(x\)         = 64

   \(x\)         = 64 : 2

   \(x\)         = 32

3x - 28 = x+36

3x - x = 36+28

2x      =64

x=64:2

x=32

Tỉ số bạn nữ và bạn nam là: 12: 15 = \(\dfrac{12}{15}\) 

Ta có sơ đồ:

Theo sơ đồ ta có:

Số bạn nam là: 135:(12+15) \(\times\)15 = 75 (bạn)

Số ban nữ là: 135 - 75 = 60 (bạn)

Đáp số: nữ 60 bạn

             nam 75 bạn

Tổng số phần bằng nhau là:

12 + 15 = 27 ( phần )

Có số bạn nam là:

135 : 27 x 15 = 75 ( bạn nam )

Có số bạn nữ là:

135 - 75 = 60 ( bạn nữ )

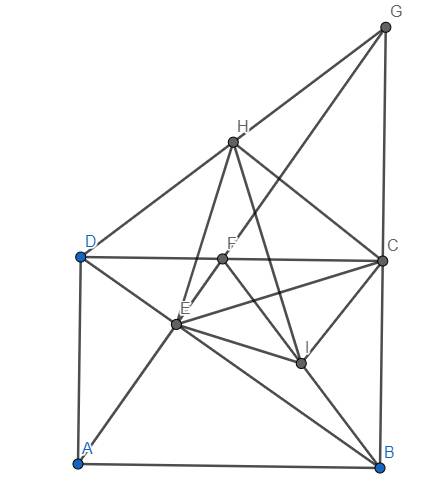
a) Ý 1: Dựa vào \(\widehat{AEB}=\widehat{DAB}=90^o\) và \(\widehat{ABD}\) chung, suy ra \(\Delta ABE~\Delta DBA\left(g.g\right)\)

  Ý 2: Từ \(\Delta ABE~\Delta DBA\Rightarrow\dfrac{AB}{BD}=\dfrac{BE}{AB}\Rightarrow AB^2=BE.BD\)

b) Dễ thấy \(\widehat{DEF}=\widehat{BEG}=90^o\) và \(\widehat{DFE}=\widehat{EBG}\) (vì cùng phụ với \(\widehat{BDC}\)) nên suy ra \(\Delta EDF~\Delta EGB\left(g.g\right)\) \(\Rightarrow\dfrac{ED}{EG}=\dfrac{EF}{EB}\) \(\Rightarrow EG.EF=ED.EB\)   (1)

 Mặt khác, dễ dàng cm \(\Delta EAD~\Delta EBA\left(g.g\right)\) \(\Rightarrow\dfrac{EA}{EB}=\dfrac{ED}{EA}\) \(\Rightarrow EA^2=EB.ED\)    (2)

Từ (1) và (2) \(\Rightarrow EA^2=EG.EF\left(=EB.ED\right)\)

c) Dễ thấy F là trực tâm của \(\Delta GBD\). \(\Delta GED\) vuông tại E có trung tuyến EH nên \(EH=\dfrac{1}{2}DG\). Tương tự suy ra \(CH=\dfrac{1}{2}DG\). Từ đó \(EH=DH\). Suy ra H nằm trên đường trung trực của đoạn CE  (3)

 Mặt khác, \(\Delta EBF\) vuông tại E có trung tuyến EI nên \(EI=\dfrac{1}{2}BF\). Tương tự, ta có \(CI=\dfrac{1}{2}BF\). Do đó \(EI=CI\) hay I nằm trên đường trung trực của đoạn CE   (4)

 Từ (3) và (4), suy ra HI là đường trung trực của đoạn CE, suy ra \(HI\perp CE\) (đpcm)

Hình vẽ đây nhé

Hôm nay olm.vn  sẽ hướng dẫn em cách giải toán nâng cao chuyển động trên dòng nước em nhé.

Kiến thức cần nhớ: V_xuôi = V_thuyền + V_nước

                                      V_ngược = V_thuyền - V_nước

                                V_xuôi + V_ngược = V_nước \(\times\) 2

                                    Giải:

Đổi 1 giờ 10 phút = \(\dfrac{7}{6}\)giờ;    1 giờ 30 phút = 1,5 giờ

Cứ 1 giờ thuyền xuôi dòng được: 1 : \(\dfrac{7}{6}\) = \(\dfrac{6}{7}\)(quãng sông)

Cứ 1 giờ thuyền ngược dòng được: 1: 1,5 = \(\dfrac{2}{3}\) (quãng sông)

Hiệu vận tốc thuyền xuôi dòng với vận tốc thuyền đó ngược dòng là:

               5  \(\times\)  2 = 10 (km)

10 km ứng với phân số là: \(\dfrac{6}{7}\) - \(\dfrac{2}{3}\) = \(\dfrac{4}{21}\)(quãng sông)

Quãng sông dài là: 10 : \(\dfrac{4}{21}\) = 52,5 (km)

Đáp số: 52,5 km

Đổi 1 giờ 10 phút = \(\dfrac{7}{6}\) giờ 

1 giờ 30 phút = \(\dfrac{3}{2}\) giờ 

Quy đồng hai mẫu số chung cùng tử số ta được: \(\dfrac{7}{6}=\dfrac{21}{18}\) và \(\dfrac{3}{2}=\dfrac{21}{14}\)

Vận tốc xuôi dòng sẽ là: \(\dfrac{21}{14}:\dfrac{21}{18}=\dfrac{18}{14}\) km/h 

Hiệu số vận tốc là: 5 x 2 = 10 km/h 

Vận tốc của chiếc thuyền khi ngược dòng là: 

10 : ( 18 - 14 ) x 14 = 35 km/h 

Chiều dài quãng sông là: 

35 x 3 : 2 = 52,5 km

Nếu thêm 2 đv vào thừa số t2 thì tích sẽ tăng lên 2 lần thừa số thứ nhất

Theo bài ra, 2 lần thừa số thứ nhất là : 32

Thừa số t1 là :

    32:2=16 

Thừa số t2 là :

    96:16=6

Vậy 2 spt là : 16 và 6

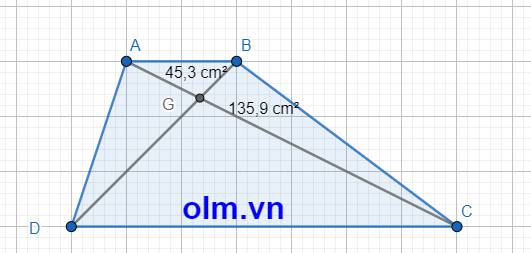
Hai tam giác ABD và tam giác ABC có chiều cao bằng nhau và chung cạnh đáy AB nên:

S_ABD = S_ABC = S_ABG + S_BCG = S_ABG + S_ADG 

⇒ S_BCG = S_ADG = 135,9 cm²

Hai tam giác ABG và tam giác BGC có chung chiều cao hạ từ đỉnh B xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và bằng:

\(\dfrac{AG}{GC}\) = \(\dfrac{45,3}{135,9}\) = \(\dfrac{1}{3}\)

Hai tam giác ADG và tam giác DCG có chung chiều cao hạ từ đỉnh D xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và bằng:

\(\dfrac{AG}{GC}\) = \(\dfrac{1}{3}\) ⇒ S_ADG  = \(\dfrac{1}{3}\)S_DCG ⇒S_DCG  = 135,9\(\times\)3 = 407,7 (cm²)

Diện tích hình thang ABCD là:

45,3 + 135,9 + 135,9 + 407,7 = 724,8 (cm²)

Đáp số 724,8 cm²

ĐKXĐ : \(\left\{{}\begin{matrix}x\ne2\\x\ne4\end{matrix}\right.\)

\(\dfrac{x-3}{x-2}+\dfrac{x-2}{x-4}=-1\)

\(\Leftrightarrow\left(x-3\right).\left(x-4\right)+\left(x-2\right)^2=-\left(x-2\right).\left(x-4\right)\)

\(\Leftrightarrow3x^2-17x+24=0\)

\(\Leftrightarrow3x^2-9x-8x+24=0\)

\(\Leftrightarrow\left(3x-8\right)\left(x-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}3x-8=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{3}\\x=3\end{matrix}\right.\left(\text{thỏa}\right)\)

\(\dfrac{x-3}{x-2}+\dfrac{x-2}{x-4}=-1\left(x\ne\left\{2;4\right\}\right)\\ =>\dfrac{\left(x-3\right)\left(x-4\right)+\left(x-2\right)^2}{\left(x-2\right)\left(x-4\right)}=-1\\ =>x^2-3x-4x+12+x^2-4x+4=-\left(x-2\right)\left(x-4\right)\\ =>2x^2-11x+16=-x^2+6x-8\\ =>3x^2-17x+24=0\\ =>\left(x-3\right)\left(3x-8\right)=0\\ =>\left[{}\begin{matrix}x=3\\x=\dfrac{8}{3}\end{matrix}\right.\left(TMDK\right)\)

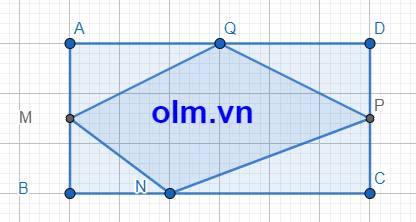
S_AMQ = \(\dfrac{1}{2}\)AM\(\times\)AQ  = \(\dfrac{1}{2}\times\) \(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{2}\)AD = \(\dfrac{1}{8}\)\(\times\)S_ABCD

S_DPQ = \(\dfrac{1}{2}\)DQ\(\times\)DP   = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{1}{2}\) AD\(\times\)\(\dfrac{1}{2}\)DP = \(\dfrac{1}{8}\) \(\times\) S_ABCD

CN    =   CB - BN     = CB - \(\dfrac{1}{3}\)CB = \(\dfrac{2}{3}\)CB

S_CPN = \(\dfrac{1}{2}\)CP\(\times\)CN   =  \(\dfrac{1}{2}\)\(\times\)\(\dfrac{1}{2}\) CD\(\times\)\(\dfrac{2}{3}\)CB = \(\dfrac{1}{6}\)S_ABCD

S_BNM = \(\dfrac{1}{2}\)BN\(\times\)BM   = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{3}\)BC    = \(\dfrac{1}{12}\)S_ABCD

Diện tích tứ giác MNPQ bằng:  (1 - \(\dfrac{1}{8}\) - \(\dfrac{1}{8}\) - \(\dfrac{1}{6}\) - \(\dfrac{1}{12}\) )S_ABCD = \(\dfrac{1}{2}\)S_ABCD

Diện tích của tứ giác MNPQ là: 240\(\times\)\(\dfrac{1}{2}\) = 120 (cm²)