Gọi số cần tìm là \(\overline{ab3}\)

Ta có : 

\(\overline{ab32}-\overline{ab3}=4079\\ \overline{ab3}\cdot10+2-\overline{ab3}=4079\\ \overline{ab3}\cdot\left(10-1\right)=4079-2\\ \overline{ab3}\cdot9=4077\\ \overline{ab3}=4077:9\\ \overline{ab3}=453\)

Vậy số cần tìm là 453

Gọi thương là b

Ta có: a = b20 + 17

=> a+1 = b20 + 17 + 1 = b20 + 18

b20 ⋮ 2 ; 18 ⋮ 2 => (b20 + 18) ⋮ 2

đã CMR : a+1  ⋮ 2

` @ L I N H `

Gọi thương là b

Ta có: a = b20 + 17

=> a+1 = b20 + 17 + 1 = b20 + 18

b20 ⋮ 2 ; 18 ⋮ 2 => (b20 + 18) ⋮ 2

đã CMR : a+1  ⋮ 2

\(-\dfrac{2}{3}\cdot x+75\%-x=-2\)

\(x\cdot\left(-\dfrac{2}{3}-1\right)+0,75=-2\)

\(x\cdot\left(-\dfrac{5}{3}\right)=-2-0,75\)

\(x\cdot\left(-\dfrac{5}{3}\right)=-\dfrac{11}{4}\)

\(x=-\dfrac{11}{4}\cdot\left(-\dfrac{3}{5}\right)\)

\(x=\dfrac{33}{20}\)

2023.2021=2022.2021+2021>2022.2020

2021.2023 

= (2020+1).(2022+1)

=2020.2022 +(2020+2022+1)

mà (2020+2022+1) >1

⇒ 2021.2023 > 2022.2020

\(41\cdot\left(2x-8\right)=0\)

\(\Rightarrow2x-8=0\)

\(\Rightarrow2x=8\)

\(\Rightarrow x=\dfrac{8}{2}=4\)

41.(2x-8)=0

      2x-8=0:41

      2x-8=0

      2x   =0+8

      2x   =8

        x   =8:2

        x=4

vậy x=4

\(1+2+3+...+x=45\)

\(\Rightarrow\left(x+1\right)\cdot\dfrac{\left(x-1\right):1+1}{2}=45\)

\(\Rightarrow\left(x+1\right)\cdot\dfrac{x}{2}=45\)

\(\Rightarrow x\cdot\dfrac{x}{2}+\dfrac{x}{2}=45\)

\(\Rightarrow\dfrac{x^2+x}{2}=45\)

\(\Rightarrow x^2+x=90\)

\(\Rightarrow x=9\)

B = 99999.65

vì 65 : 13 = 5

B = 99999.5.13

B chia hết cho 13

Vì tấm bìa được cắt hết => cạnh của hình vuông là ước chung của chiều dài và chiều rộng hình chữ nhật.

Khi đó độ dài cạnh hình vuông lớn nhất chính là ƯCLN của chiều dài và chiều rộng hình chữ nhật.

Ta có: 60 = 22.3.5

 96 = 25.3

ƯCLN(60;96) = 22.3 = 12

Cạnh hình vuông là 12 cm

Diện tích tấm bìa hình chữ nhật là 96 x 60 = \(5760\left(cm^2\right)\)

Để cắt tấm bìa thành a mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết và cạnh hình vuông có độ dài lớn nhất là b (cm) thì a phải là số nhỏ nhất sao cho \(5760:a=b^2\) 

Mà \(5760=2^7.3^2.5=\left(2^6.3^2\right).\left(2.5\right)\)

\(=\left(8^2.3^2\right).10=24^2.10\)

Nên khi số mảnh lớn nhất là a = 10 thì cạnh hình vuông có độ dài lớn nhất là 24 cm

\(5760=24^2.10\)

\(5760=24^2.10\)

`@` `\text {Ans}`

`\downarrow`

`(6 - 2 4/5)*3 1/8 - 3 1/5 \div 1/4`

`= 16/5*3 - 64/5`

`= 48/5 - 64/5`

`= -16/5`

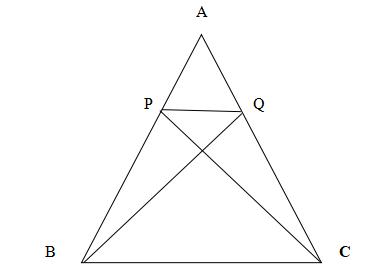
a/

Hai tg BPQ và tg CQP có đường cao từ B->PQ = đường cao từ C->PQ

Cạnh đáy PQ chung

\(\Rightarrow S_{BPQ}=S_{CQP}\)

Hai tg trên có phần diện tích chung là \(S_{IPQ}\Rightarrow S_{BIP}=S_{QIC}\)

b/

Hai tg ACP và tg ABC có chung đường cao từ C->AB nên

\(\dfrac{S_{ACP}}{S_{ABC}}=\dfrac{AP}{AB}=\dfrac{1}{3}\Rightarrow S_{ACP}=\dfrac{1}{3}xS_{ABC}\)

Hai tg ACP và tg ABQ có phần diện tích chung là \(S_{APIQ}\)

Mà \(S_{BIP}=S_{QIC}\Rightarrow S_{ACP}=S_{ABQ}=\dfrac{1}{3}xS_{ABC}\)

Hai tg APQ và tg ABQ có chung đường cao từ Q->AB nên

\(\dfrac{S_{APQ}}{S_{ABQ}}=\dfrac{AP}{AB}=\dfrac{1}{3}\Rightarrow S_{APQ}=\dfrac{1}{3}xS_{ABQ}=\dfrac{1}{3}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{9}xS_{ABC}\)

\(\Rightarrow S_{BPQC}=S_{ABC}-S_{APQ}=S_{ABC}-\dfrac{1}{9}xS_{ABC}=\dfrac{8}{9}xS_{ABC}=\dfrac{8}{9}x45=40cm^2\)