So sánh 71^50 và 37^75
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2^{300}=\left(2^3\right)^{100}=8^{100}\\ 3^{200}=\left(3^2\right)^{100}=9^{100}\\ Vì:8^{100}< 9^{100}\Rightarrow2^{300}< 3^{200}\)

B = \(\dfrac{1}{2002}\) + \(\dfrac{2}{2021}\) + \(\dfrac{3}{2020}\)+...+ \(\dfrac{2021}{2}\) + \(\dfrac{2022}{1}\)
B = \(\dfrac{1}{2002}\) + \(\dfrac{2}{2021}\) + \(\dfrac{3}{2020}\)+...+ \(\dfrac{2021}{2}\) + 2022
B = 1 + ( 1 + \(\dfrac{1}{2022}\)) + ( 1 + \(\dfrac{2}{2021}\)) + \(\left(1+\dfrac{3}{2020}\right)\)+ ... + \(\left(1+\dfrac{2021}{2}\right)\)
B = \(\dfrac{2023}{2023}\) + \(\dfrac{2023}{2022}\) + \(\dfrac{2023}{2021}\) + \(\dfrac{2023}{2020}\) + ...+ \(\dfrac{2023}{2}\)
B = 2023 \(\times\) ( \(\dfrac{1}{2023}\) + \(\dfrac{1}{2022}\) + \(\dfrac{1}{2021}\) + \(\dfrac{1}{2020}\)+ ... + \(\dfrac{1}{2}\))
Vậy B > C

\(A=\dfrac{1}{2}-\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3-\left(\dfrac{1}{2}\right)^4+...+\left(\dfrac{1}{2}\right)^{2023}-\left(\dfrac{1}{2}\right)^{2024}\)
\(A=\dfrac{2}{2^2}-\dfrac{1}{2^2}+\dfrac{2}{2^4}-\dfrac{1}{2^4}+...+\dfrac{2}{2^{2024}}-\dfrac{1}{2^{2024}}\)
\(A=\dfrac{1}{2^2}+\dfrac{1}{2^4}+\dfrac{1}{2^6}+...+\dfrac{1}{2^{2024}}\)
\(A=\dfrac{2^{2022}}{2^{2024}}+\dfrac{2^{2020}}{2^{2024}}+\dfrac{2^{2018}}{2^{2024}}+...+\dfrac{1}{2^{2024}}\)
\(2^2A=\dfrac{2^{2024}}{2^{2024}}+\dfrac{2^{2022}}{2^{2024}}+\dfrac{2^{2020}}{2^{2024}}+...+\dfrac{2^2}{2^{2024}}\)
\(\Rightarrow4A-A=3A=1-\dfrac{2}{2^{2024}}-\dfrac{1}{2^{2024}}\)
\(3A=1-\left(\dfrac{2}{2^{2024}}+\dfrac{1}{2^{2024}}\right)\)
\(3A=1-\dfrac{3}{2^{2024}}\)
\(A=\dfrac{1-\dfrac{3}{2^{2024}}}{3}\)
\(A=\dfrac{3\left(\dfrac{1}{3}-\dfrac{1}{2^{2024}}\right)}{3}\)
\(A=\dfrac{1}{3}-\dfrac{1}{2^{2024}}\)

\(\dfrac{4}{x}=\dfrac{x}{16}\\ \Leftrightarrow x.x=4.16\Leftrightarrow x^2=64\\ \Leftrightarrow\left[{}\begin{matrix}x^2=8^2\\x^2=\left(-8\right)^2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
=> x\(\) . x = 4 . 16 => x2 = 64 => x2 = 82 => x = 8 vậy x = 8

\(12-12\dfrac{1}{3}=12-\dfrac{12\times3+1}{3}=12-\dfrac{37}{3}=\dfrac{12\times3-37}{3}=\dfrac{36-37}{3}=\dfrac{-1}{3}\)

Lời giải:
Gọi tổng trên là $A$
$A=2(\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.11}+...+\frac{1}{100.103})$
$A=\frac{2}{3}(\frac{3}{1.4}+\frac{3}{4.7}+\frac{3}{7.11}+...+\frac{3}{100.103})$
$=\frac{2}{3}(\frac{4-1}{1.4}+\frac{7-4}{4.7}+...+\frac{103-100}{100.103})$
$=\frac{2}{3}(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+....+\frac{1}{100}-\frac{1}{103})$
$=\frac{2}{3}(1-\frac{1}{103})$
$=\frac{2}{3}.\frac{102}{103}=\frac{68}{103}$
Bạn Akai Haruma đáp án của bạn đúng khi phân số 1/7*11 là 1/7*10

\(65\%=\dfrac{13}{20}\\ Nghịch.đảo.của.65\%:\dfrac{20}{13}\)
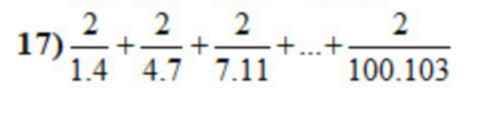
\(71^{50}=71^{2.25}=\left(71^2\right)^{25}=5041^{25}\\ 37^{75}=37^{3.25}=\left(37^3\right)^{25}=50653^{25}\\ Vì:5041^{25}< 50653^{25}\Rightarrow71^{50}< 37^{75}\)