Tìm nghiệm nguyên: (x + 1)(x + 3)(x + 5)(x + 7) + 3y3 = 2023
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
H
14 tháng 4 2023
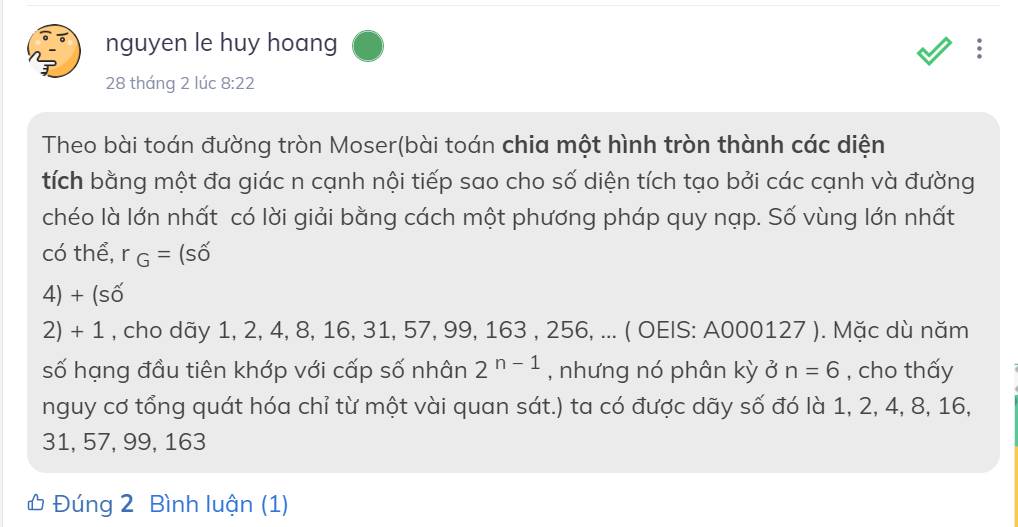
1. Ta chọn $x=3k;y=4k;z=5k$ với $k$ là số nguyên dương.
Khi này $x^2+y^2=25k^2 =z^2$. Tức có vô hạn nghiệm $(x;y;z)=(3k;4k;5k)$ với $k$ là số nguyên dương thỏa mãn
8 tháng 4 2023
Nếu bạn Minh biết chữ số hàng đơn vị và bạn Bình không biết chữ số hàng đơn vị thì bạn Bình không thể đảm bảo bạn Minh không biết với trường hợp hàng đơn vị là 7 hoặc 9
=> Bạn Bình biết chữ số hàng đơn vị
Mà bạn Bình chưa xác định được mật khẩu
=> Hàng đơn vị không phải 7 hoặc 9
=> Loại 1119 và 1107
Nếu bạn Bình biết cả hàng chục và hàng đơn vị mà hàng chục và hàng đơn vị của các số không trùng nhau thì bạn Bình sẽ xác định được mật khẩu trước khi bạn Minh nói
=> Bạn Bình không biết hàng chục
=> Bạn Minh biết hàng chục
Hàng chục có 4 TH: 0; 1; 2; 3
Có 3 số có hàng chục là 3 (1134; 1135; 1138); 2 số có hàng chục là 2 (1124; 1126); 2 số có hàng chục là 0 (1105; 1106)
Nếu hàng chục là 0; 2 hoặc 3 thì Minh chưa thể xác định được mật khẩu
=> Hàng chục là 1
Chỉ có 2 số có hàng chục là 1 là 1119 và 1118 mà 1119 đã bị loại
=> Mật khẩu là 1118
QT
Quoc Tran Anh Le
Giáo viên
9 tháng 4 2023
1GP cho sự nỗ lực của bạn, bạn thử lại bạn nhé!
24 tháng 3 2023
Rep bài viết sơm, Chúc mn cuối tuần vv .
Tranh thủ e vào xin ít vía cho tối nay cho lên top ak.
\(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+3y^3=2023\)
\(\Leftrightarrow\left[\left(x+1\right)\left(x+7\right)\right]\left[\left(x+3\right)\left(x+5\right)\right]+3y^3=2023\)
\(\Leftrightarrow\left(x^2+8x+7\right)\left(x^2+8x+15\right)+3y^3=2023\) (*)
Đặt \(x^2+8x+11=t\left(t\inℤ;t\ge-5\right)\), pt (*) trở thành \(\left(t-4\right)\left(t+4\right)+3y^3=2023\)
\(\Leftrightarrow t^2-16+3y^3=2023\)
\(\Leftrightarrow t^2+3y^3=2039\) (1)
Xét pt (1), dễ thấy \(t^2\equiv0\left(mod3\right)\) hoặc \(t^2\equiv1\left(mod3\right)\), lại có \(3y^3\equiv0\left(mod3\right)\) nên \(VT\equiv0\left(mod3\right)\) hoặc \(VT\equiv1\left(mod3\right)\). Nhưng \(VP=2039\equiv2\left(mod3\right)\), điều này có nghĩa là (1) vô nghiệm.
Vậy phương trình đã cho không thể có nghiệm nguyên.
(x+1)(x+3)(x+5)(x+7)+3y3=2023
⇔[(�+1)(�+7)][(�+3)(�+5)]+3�3=2023⇔[(x+1)(x+7)][(x+3)(x+5)]+3y3=2023
⇔(�2+8�+7)(�2+8�+15)+3�3=2023⇔(x2+8x+7)(x2+8x+15)+3y3=2023 (*)
Đặt �2+8�+11=�(�∈Z;�≥−5)x2+8x+11=t(t∈Z;t≥−5), pt (*) trở thành (�−4)(�+4)+3�3=2023(t−4)(t+4)+3y3=2023
⇔�2−16+3�3=2023⇔t2−16+3y3=2023
⇔�2+3�3=2039⇔t2+3y3=2039 (1)
Xét pt (1), dễ thấy �2≡0(���3)t2≡0(mod3) hoặc �2≡1(���3)t2≡1(mod3), lại có 3�3≡0(���3)3y3≡0(mod3) nên ��≡0(���3)VT≡0(mod3) hoặc ��≡1(���3)VT≡1(mod3). Nhưng ��=2039≡2(���3)VP=2039≡2(mod3), điều này có nghĩa là (1) vô nghiệm.
Vậy phương trình đã cho không thể có nghiệm nguyên