
Câu 1:
Cho các biểu thức \(A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}\) và \(B=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{11\sqrt{x}-3}{x-9};\) với \(x\ge0;x\ne9.\)
a) Tính giá trị của A khi x = 36;
b) Rút gọn biểu thức M = A + B;
c) Tìm x sao cho M = M4.
Câu 2:
a) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Trên quãng đường AB dài 200km có hai ô tô đi ngược chiều. Xe 1 khởi hành từ A đi đến B, xe 2 khởi hành từ B đi đến A. Hai xe khởi hành cùng một lúc và sau hai giờ thì gặp nhau. Tính vận tốc mỗi xe nếu vận tốc xe 2 lớn hơn vận tốc xe 1 là 10km/h.
b) Một hộp sữa hình trụ có thể tích là 16π (cm3). Biết rằng đường kính đáy và độ dài trục của hình trụ bằng nhau.
Tính diện tích vật liệu cần dùng để tạo nên một hộp sữa như vậy (bỏ qua diện tích phần ghép nối).
Câu 3:
1) Cho đường thẳng (d): y = mx - m + 1 và parabol (P): y = x2;
a) Tìm m để đường thẳng (d) vad parabol (P) cắt nhau tại hai điểm phân biệt;
b) Gọi \(x_1, x_2\) là hoành độ các giao điểm của (d) và (P). Tìm m sao cho \(x_1^2x_2+x_2^2x_1=2.\)
2) Giải hệ phương trình \(\left\{{}\begin{matrix}\dfrac{3}{x}+y=5\\\dfrac{2}{x}-2y=-2.\end{matrix}\right.\)
Câu 4:
Cho nửa đường tròn (O; R) đường kính AB. Trên cùng nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ hai tiếp tuyến Ax, By với nửa đường tròn. Lấy điểm M thuộc nửa đường tròn, tiếp tuyến tại M của nửa đường tròn cắt Ax, By lần lượt tại C và D. Nối AD cắt BC tại N, MN cắt AB tại H.
a) Chứng minh OACM là tứ giác nội tiếp;
b) Chứng minh tích AC.BD không phụ thuộc vào vị trí của M;
c) Chứng minh MN // BD và MN = NH.
Câu 5:
Cho a, b, c > 0; a + b + c = 3. Tìm giá trị nhỏ nhất của biểu thức:
\(M=\dfrac{ab}{c^2\left(a+b\right)}+\dfrac{ac}{b^2\left(a+c\right)}+\dfrac{bc}{a^2\left(b+c\right)}.\)
Chúc các em ôn thi tốt và đạt điểm cao trong kì thi sắp tới!




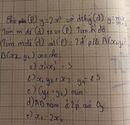
5.
Không mất tính tổng quát, giả sử \(c=min\left\{a;b;c\right\}\Rightarrow0\le c\le1\Rightarrow1-\dfrac{c}{2}>0\)
\(P=bc+ca+ab\left(1-\dfrac{c}{2}\right)\ge0\)
\(P_{min}=0\) khi \(\left(a;b;c\right)=\left(0;0;3\right)\) và các hoán vị
\(P=c\left(a+b\right)+ab\left(1-\dfrac{c}{2}\right)\le c\left(3-c\right)+\dfrac{\left(a+b\right)^2}{4}\left(1-\dfrac{c}{2}\right)\)
\(P\le3c-c^2+\dfrac{\left(3-c\right)^2}{4}\left(1-\dfrac{c}{2}\right)\)
\(P\le\dfrac{5}{2}-\dfrac{c^3}{8}+\dfrac{3c}{8}-\dfrac{1}{4}=\dfrac{5}{2}-\dfrac{1}{8}\left(c-1\right)^2\left(c+2\right)\le\dfrac{5}{2}\)
\(P_{max}=\dfrac{5}{2}\) khi \(a=b=c=1\)
Cách 2 phần tìm max bài 5:
Áp dụng BĐT: \(abc\ge\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\)
\(\Leftrightarrow abc\ge\left(3-2a\right)\left(3-2b\right)\left(3-2c\right)\)
\(\Leftrightarrow abc\ge-8abc+12\left(ab+bc+ca\right)-27\)
\(\Leftrightarrow3abc+27\ge12\left(ab+bc+ca\right)-6abc\)
\(\Leftrightarrow ab+bc+ca-\dfrac{1}{2}abc\le\dfrac{abc}{4}+\dfrac{9}{4}\le\dfrac{1}{4}.\left(\dfrac{a+b+c}{3}\right)^3+\dfrac{9}{4}=\dfrac{5}{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)