Cho hình vẽ sau:
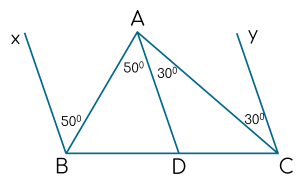
Chứng minh $Bx$ // $Cy$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


số tiền lãi mà mẹ minh được nhận sau 6 tháng là
2062400 - 2000000 = 62400 (đồng)
mỗi tháng số tiền lãi mà mẹ minh nhận được là
62400 : 6 = 10400 (đồng)
% lãi hàng tháng là
10400 : 2000000 x 100 = 0,52%
đs....
số tiền lãi mà mẹ minh được nhận sau 6 tháng là
2062400 - 2000000 = 62400 (đồng)
mỗi tháng số tiền lãi mà mẹ minh nhận được là
62400 : 6 = 10400 (đồng)
% lãi hàng tháng là
10400 : 2000000 x 100 = 0,52%


Bài hát mà em thích nhất chắc có lẽ là bài " The nights`, nó mang lại cảm giác thư giản sau giờ học mệt mỏi, hoặc là sau khi làm 1 công việc nào đó, từ những nội dung của bài hát và người hát có thể khiến ta cảm thấy an tâm, cảm thấy dễ ngủ, những giai điệu nhẹ nhàng cuốn hút, những lời hát hay và nhẹ rất có ý nghĩa trong cuộc sống (:

a)
\(\begin{matrix}N\left(x\right)=-4x^4+9x^3-x^2+5x+\dfrac{1}{3}\\^-M\left(x\right)=-x^4-9x^3+x^2+9x+\dfrac{4}{3}\\\overline{N\left(x\right)-M\left(x\right)=-3x^4+18x^3-2x^2-4x-1}\end{matrix}\)
b)
\(\begin{matrix}M\left(x\right)=-x^4-9x^3+x^2+9x+\dfrac{4}{3}\\^+N\left(x\right)=-4x^4+9x^3-x^2+5x+\dfrac{1}{3}\\\overline{M\left(x\right)+N\left(x\right)=-5x^4+14x+\dfrac{5}{3}}\end{matrix}\)

Rõ ràng các góc $\angle AOD,\angle BOC $ được đề cập là các góc không lớn hơn $180^o$.
Khi đó ta thấy rằng $\angle AOD,\angle BOC$ là hai góc đối đỉnh nên $\angle AOD=\angle BOC$, từ đó kết hợp giả thiết ta thu được $2\angle AOD=100^o$ hay $\angle AOD=\angle BOC=50^o$
Khi đó $\angle BOD=\angle AOC=180^o-\angle 50^o=130^o$

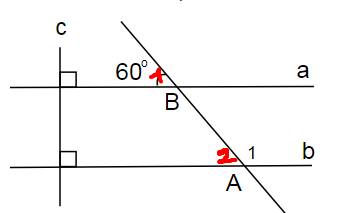
Vì a \(\perp\) c và b \(\perp\) c nên a//b
=>\(\hat{B_1}=\hat{A_2}\)=600 (hai góc đồng vị)
Mà \(\hat{A_2}\) và \(\hat{A_1}\)là hai góc kề bù
=> \(\hat{A_1}+\hat{A_2}=180^o\)
hay \(\hat{A_1}\) + 60o=180o
=> \(\hat{A_1}\) = 180o-60o=120o
Vậy \(\hat{A_1}\)=1200
Vì \(\widehat{xBA}=\widehat{BAD}\left(=50^o\right)\) mà \(\widehat{xBA}\text{ và }\widehat{BAD}\) là 2 góc so le trong
=> Bx//AD (1)
Vì \(\widehat{DAC}=\widehat{ACy}\left(=30^o\right)\) mà \(\widehat{DAC}\text{ và }\widehat{ACy}\) là 2 góc so le trong
=> AD // Cy (2)
Từ (1) và (2) => Bx // Cy
Ta có:
`@` \(\widehat{ABx}=\widehat{DAB}=50^o\)
`=>Bx////AD` ( 2 góc so le trong bằng nhau ) (1)
`@`\(\widehat{ACy}=\widehat{DAC}=30^o\)
`=>Cy////AD` ( 2 góc so le trong bằng nhau ) (2)
\(\left(1\right);\left(2\right)\Rightarrow\)`Bx////Cy`