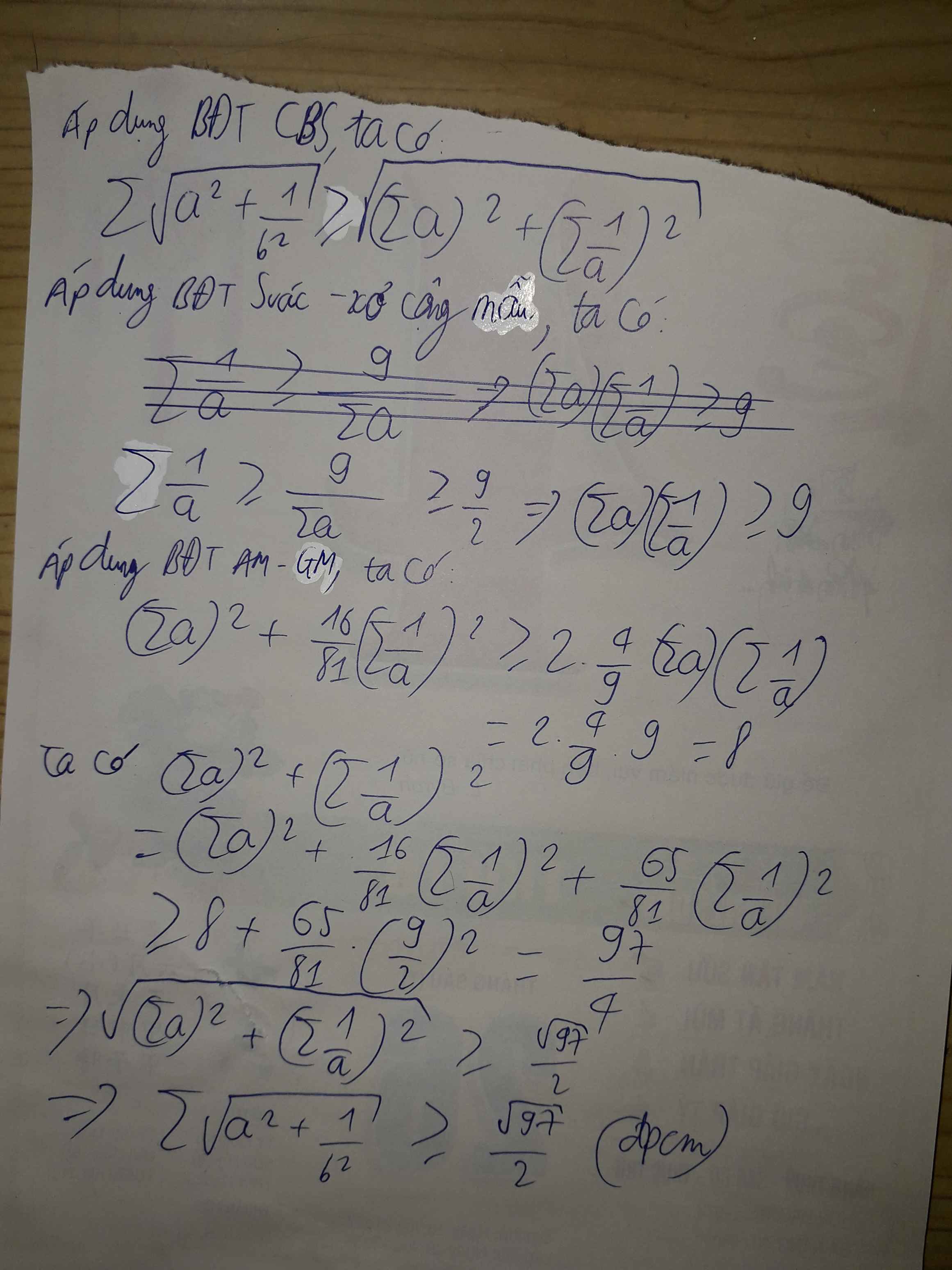Các bạn có biết không, từ ngày 5/8 - 11/8 cứ mỗi 100 bạn bè mời được (và chụp màn hình trước và sau khi mời gửi về cho page) thì bạn nhận được 8 điểm lận đó. Xem chi tiết tại: (1) Cuộc thi Trí tuệ VICE - Bài viết | Facebook. Mời ngay thôi nào!
[Toán.C33|5.8.2021| Hir Dương (Facebook)]
1)

2)

3)
4) 
5) 
#vice



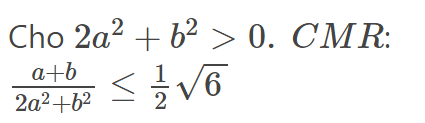
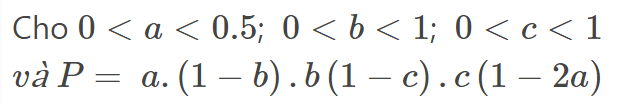
 4)
4) 






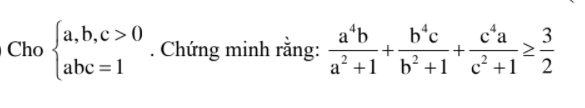
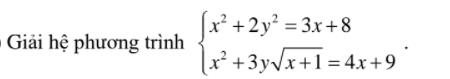
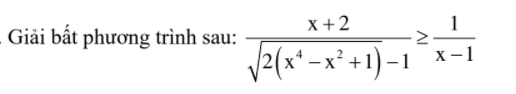
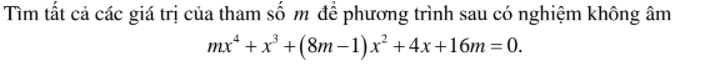

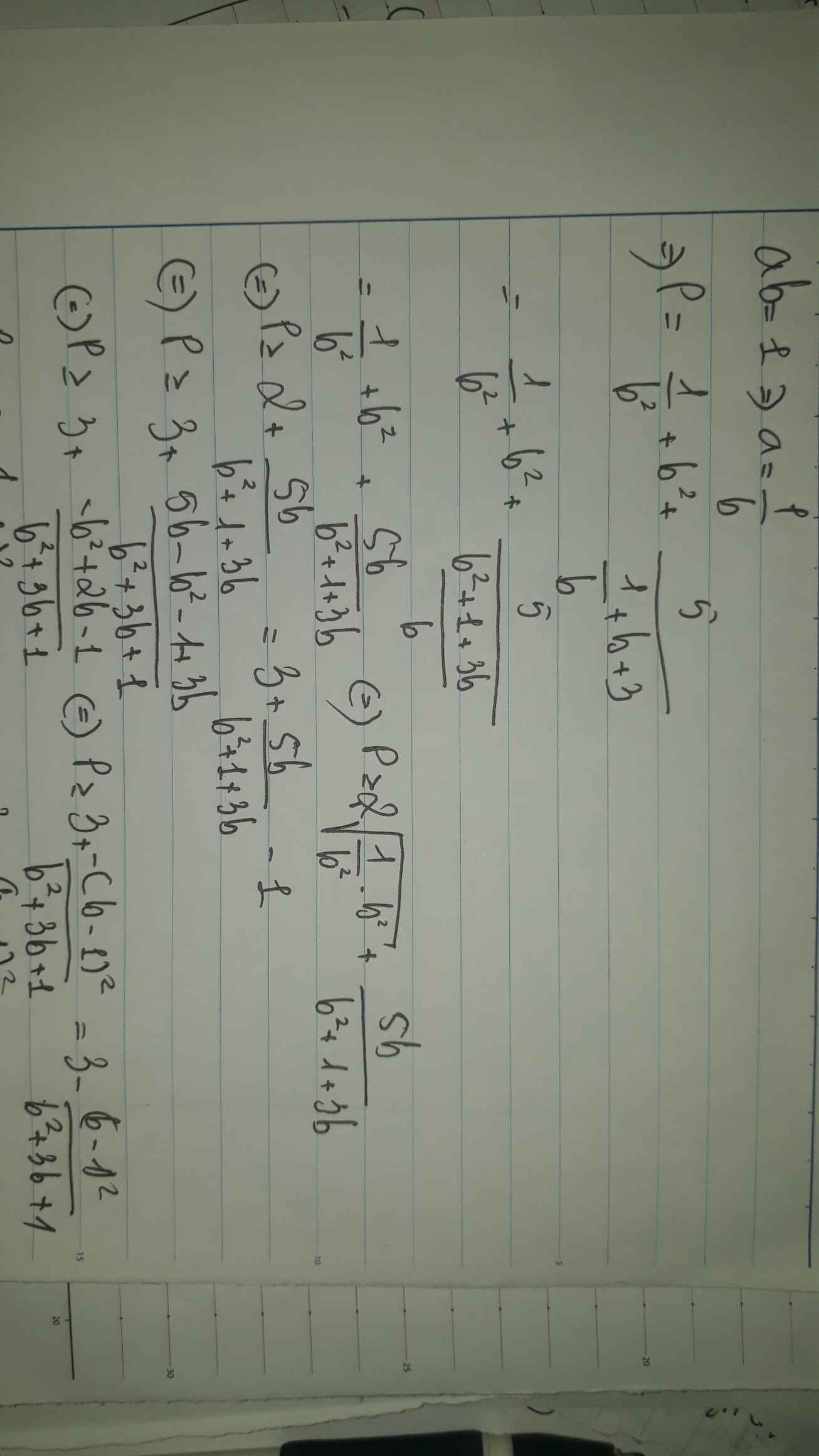
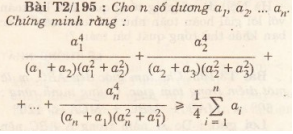
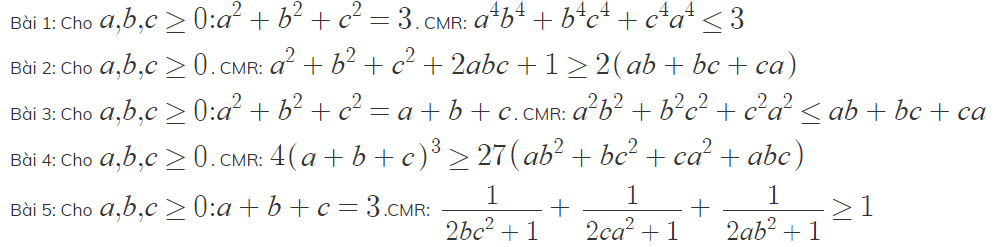


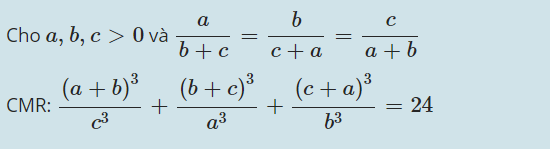
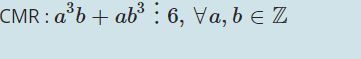
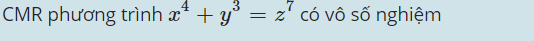

1
đặt biểu thức cần chứng minh là P
có \(\sqrt{a^2+\dfrac{1}{b^2}}=\dfrac{1}{\sqrt{97}}.\sqrt{\left(a^2+\dfrac{1}{b^2}\right).\left(4^2+9^2\right)}\ge\dfrac{1}{\sqrt{97}}\left(4a+\dfrac{9}{b}\right)\)
là tương tự đối với \(\sqrt{b^2+\dfrac{1}{c^2}},\sqrt{c^2+\dfrac{1}{a^2}}\)
\(=>P\ge\)\(\dfrac{1}{\sqrt{97}}\left(4a+\dfrac{9}{b}+4b+\dfrac{9}{c}+4c+\dfrac{9}{a}\right)\)
(đến đây thấy đề sai sai vì ngược dấu )
Toán C33), bài 1