Cho tam giác ABC, các điểm M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Gọi O, I, D lần lượt là giao điểm của CM với PN, của AO với BC, của MI với AC. CM : AI, BD, MP đồng quy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ DI ║ BC. Áp dụng hệ quả định lý Ta-lét vào ΔABC
⇒AD /AB =AI/AC
⇒DB/AB=IC/AC
⇒IC/DB=AC/AB
Vì MC║DI. Áp dụng định lý Ta-lét vào ΔDIE
⇒DM/ME=IC/CE
Mà DM=CE ⇒IC/CE=IC/DB
⇒DM/ME=AC/AB
Giải thích các bước giải:
Kẻ DI ║ BC. Áp dụng hệ quả định lý Ta-lét vào ΔABC
⇒AD /AB =AI/AC
⇒DB/AB=IC/AC
⇒IC/DB=AC/AB
Vì MC║DI. Áp dụng định lý Ta-lét vào ΔDIE
⇒DM/ME=IC/CE
Mà DM=CE ⇒IC/CE=IC/DB
⇒DM/ME=AC/AB

\(x^2-\left(y-3\right)x-2y-1=0\)
\(\Leftrightarrow y\left(x+2\right)=x^2+3x-1\)
Dễ thây \(x\ne-2\)
\(\Rightarrow y=\frac{x^2+3x-1}{x+2}=x+1-\frac{3}{x+2}\)
Để y nguyên thì x + 2 là ươc của 3 hay
\(\left(x+2\right)=\left\{-3;-1;1;3\right\}\)
\(x^2-\left(y-3\right)x-2y-1=0\)
\(\Leftrightarrow x^2-xy+3x-2y-1=0\)
\(\Leftrightarrow\left(x^2-xy\right)+\left(2x-2y\right)+x-1=0\)
\(\Leftrightarrow x\left(x-y\right)+2\left(x-y\right)+\left(x+2\right)-3=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-y\right)+\left(x+2\right)=3\)
\(\Leftrightarrow\left(x+2\right)\left(x-y+1\right)=3\)
Ta có x, y \(\in\) Z nên x + 2 là ước của 3 \(\Rightarrow x+2\in\left\{1;3;-1;-3\right\}\). Ta có bảng sau:
| x + 2 | x - y + 1 | x | y |
| 1 | 3 | -1 | -3 |
| 3 | 1 | 1 | 1 |
| -1 | -3 | -3 | 1 |
| -3 | -1 | -5 | -3 |

Cho tam giác ABC vuông tại A có AC>AB. Đường cao AH. Từ H kẻ HD\(\perp\)AB (D\(\in\)AB), HE\(\perp\)AC( E\(\in\)AC).a. C... - H
ctv thảo (giỏi toán của chta bên h :v) đã làm rồi. bạn nào cần thì click vào đường link xanh bên trên nhé
Gọi I là giao điểm của DE và AH.
Câu a) Ta dễ dàng chứng minh được ADHE là hình chữ nhật, sử dụng tính chất hình chữ nhật để suy ra \(\widehat{ADE}=\widehat{DAH}\)
Mà \(\widehat{DAH}=\widehat{C}\) (cùng phụ với góc ABC) nên suy ra \(\widehat{ADE}=\widehat{C}\)
Từ đó dễ dàng chứng minh được tam giác AED đồng dạng với tam giác ABC theo trường hợp góc - góc.
Câu b) Chắc là phải sử dụng lớp 9 sẽ nhanh hơn. Các bạn thử tìm thêm cách khác nhé
Chứng minh tứ giác ABNM nội tiếp suy ra \(\widehat{ANB}=\widehat{AMB}\)
Dễ dàng chứng minh được \(\widehat{AMB}=\widehat{ABC}=\widehat{AED}\)
Suy ra: \(\widehat{ANB}=\widehat{AED}\)và hai góc này ở vị trí đồng vị, suy ra: DE //BN
Câu 3. Sử dụng tỉ số đồng dạng hợp lí rồi suy ra kết quả
Ta dễ dàng chứng minh được: \(\Delta BDH\)\(\Delta BAC\).và tính được \(BD=\frac{DH.AB}{AC}\)
Chứng minh được: \(\Delta CEH\)\(\Delta CAB\).và tính được \(CE=\frac{EH.AC}{AB}\)
Chứng minh được: \(\Delta DHE\)\(\Delta BAC\).và suy ra được \(\frac{DH}{EH}=\frac{AB}{AC}\)
Suy ra: \(\frac{BD}{CE}=\frac{DH.AB}{AC}:\frac{EH.AC}{AB}=\frac{AB^2.DH}{AC^2.EH}=\frac{AB^2.AB}{AC^2.AC}\)
Vậy \(\frac{BD}{CE}=\frac{AB^3}{AC^3}\)

Bài 1:
a) đk: \(x\ne\pm2\)
b) Ta có:
\(A=\left(\frac{1}{2-x}+\frac{3x}{x^2-4}-\frac{2}{2+x}\right)\div\left(\frac{x^2+4}{4-x^2}+1\right)\)
\(A=\left[\frac{1}{2-x}-\frac{3x}{\left(2-x\right)\left(2+x\right)}-\frac{2}{2+x}\right]\div\frac{x^2+4+4-x^2}{\left(2-x\right)\left(2+x\right)}\)
\(A=\frac{2+x-3x-2\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}\div\frac{8}{\left(2-x\right)\left(2+x\right)}\)
\(A=\frac{2-2x-4+2x}{\left(2-x\right)\left(2+x\right)}\cdot\frac{\left(2-x\right)\left(2+x\right)}{8}\)
\(A=\frac{-2}{\left(2-x\right)\left(2+x\right)}\cdot\frac{\left(2-x\right)\left(2+x\right)}{8}=-\frac{1}{4}\)
=> đpcm
Bài 2:
a) đk: \(x\ne\left\{-3;0;3\right\}\)
b) Ta có:
\(B=\left[\frac{3-x}{x+3}\cdot\frac{x^2+3x+9}{\left(x-3\right)\left(x+3\right)}+\frac{x}{x+3}\right]\div\frac{3x^2}{x+3}\)
\(B=\left[\frac{-x^2-3x-9}{\left(x+3\right)^2}+\frac{x}{x+3}\right]\cdot\frac{x+3}{3x^2}\)
\(B=\frac{-x^2-3x-9+x\left(x+3\right)}{\left(x+3\right)^2}\cdot\frac{x+3}{3x^2}\)
\(B=\frac{-9}{\left(x+3\right)^2}\cdot\frac{x+3}{3x^2}\)
\(B=-\frac{3}{x\left(x+3\right)}\)
c) Khi B = 1/2 thì: \(-\frac{3}{x\left(x+3\right)}=\frac{1}{2}\)
\(\Leftrightarrow x^2+3x=-6\Leftrightarrow x^2+3x+6=0\)
\(\Leftrightarrow\left(x^2+2\cdot\frac{3}{2}\cdot x+\frac{9}{4}\right)+\frac{15}{4}=0\)
\(\Rightarrow\left(x+\frac{3}{2}\right)^2=-\frac{15}{4}\left(ktm\right)\)

Sau khi thử bằng pascal thì em thấy bài này hình như có vô số nghiệm (Chắc là sai đề). Nhưng nếu ai tìm được công thức tổng quát của k thì hay biết mấy.
Tôi xin bài này để đăng lên trang face ông nhé :)

\(\frac{x-23}{24}+\frac{x-23}{25}=\frac{x-23}{26}+\frac{x-23}{27}\)
\(\frac{x-23}{24}+\frac{x-23}{25}-\frac{x-23}{26}-\frac{x-23}{27}=0\)
\(\left(x-23\right)\left(\frac{1}{24}+\frac{1}{25}-\frac{1}{26}-\frac{1}{27}\right)=0\)
=> x-23=0
x=0+23
x=23. Vậy x=23
Chúc bạn học tốt!^_^
\(\frac{x-23}{24}+\frac{x-23}{25}=\frac{x-23}{26}+\frac{x-23}{27}\)
=> \(\frac{x-23}{24}+\frac{x-23}{25}-\frac{x-23}{26}-\frac{x-23}{27}=0\)
=>( x-13)(\(\frac{1}{24}+\frac{1}{25}-\frac{1}{26}-\frac{1}{27}\) = 0
ta thấy 1/24>1/25>1/26>1/27 => 1/24+1/25 - 1/ 26 - 1/17 > 0
=> x -13 = -
=> x=13

Em tham khảo nha.
Coi AB = 1, DC = k thì \(\frac{DO}{OB}=\frac{DC}{AB}=k\Rightarrow\frac{DO}{DB}=\frac{k}{k+1}\)
\(\Rightarrow OE=OF=\frac{k}{k+1}\Rightarrow EF=\frac{2k}{k+1}\)
Ta có \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{1}+\frac{1}{k}=\frac{k+1}{k}\)
\(\frac{2}{EF}=\frac{2}{\frac{2k}{k+1}}=\frac{k+1}{k}\)
Vậy nên \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{EF}\)

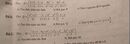
Ta thấy M,P lần lượt là trung điểm của AB,BC => MP là đường trung bình trong \(\Delta\)ABC
=> MP // AC hay MP // AD. Xét \(\Delta\)BAD có: M là trung điểm AB, MP // AD => MP đi qua trung điểm BD
Gọi MP cắt BD tại S. Khi đó S là trung điểm BD. Ta sẽ chứng minh AI đi qua S, thật vậy:
Áp dụng hệ quả ĐL Thales có: \(\frac{ON}{AM}=\frac{OP}{BM}\left(=\frac{CO}{CM}\right)\)=> ON = OP (Vì AM = BM)
Áp dụng ĐL Melelaus cho \(\Delta\)PCN và 3 điểm A,O,I có \(\frac{IP}{IC}.\frac{ON}{OP}.\frac{AC}{AN}=1\)
Thay \(\frac{ON}{OP}=1,\frac{AC}{AN}=2\), ta được \(\frac{IP}{IC}=\frac{1}{2}\). Do đó \(\frac{IC}{IB}=\frac{1}{2}\)(Vì PC=1/2BC)
Áp dụng ĐL Melelaus cho \(\Delta\)ABC và 3 điểm M,I,D có \(\frac{MA}{MB}.\frac{IC}{IB}.\frac{DA}{DC}=1\)
Thay \(\frac{MA}{MB}=1,\frac{IC}{IB}=\frac{1}{2}\)(cmt), ta được \(\frac{DA}{DC}=2\)=> C là trung điểm AD
Xét \(\Delta\)BAD: Các trung tuyến DM, BC cắt nhau tại I => I là trọng tâm của \(\Delta\)BAD
Ta có S là trung điểm BD nên AI đi qua S. Như vậy AI,BD,MP đồng quy tại trung điểm BD (đpcm).
Gọi S là giao điểm của MP và BD
Vì P là giao điểm của MS và BC
=> Tứ giác BMCS là hình bình hành
=> \(MC//BD\)
Mà M là trung điểm của AB
=> C là trung điểm của AD
CMTT S là trung điểm của BD
=> BC; DM lần lượt là trung tuyến của tam giác ABD
Mà BC giao DM tại I
=> I là trọng tâm của tam giác ABD
Mà S là trung điểm của BD
=> A;I;S thẳng hàng
=> AI;BD;MP đồng quy tại S
Vậy AI;BD;MP đồng quy tại S