Trong không gian, khẳng định nào sau đây đúng?

Khẳng định nào sau đây đúng?

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $SA \bot \left(ABCD \right)$.

Hình chiếu vuông góc của $SC$ lên mặt phẳng $ABCD$ là

Cho hình chóp tứ giác đều $S.ABCD$, có đáy $ABCD$ là hình vuông tâm $O$.

Khẳng định nào sau đây đúng?

Cho hình chóp tứ giác đều $S.ABCD$, có đáy $ABCD$ là hình vuông tâm $O$.

Khoảng cách từ $S$ đến mặt phẳng đáy là đoạn

Cho hình chóp $S.ABCD$ có đáy là hình chữ nhật. Mặt bên $\left(SAB \right)$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi $H$ là chân đường cao hạ từ đỉnh $S$ của tam giác $SAB$.

Khoảng cách từ đỉnh $S$ đến mặt đáy $\left(ABCD \right)$ là đoạn

Cho hình lập phương $ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$ (tham khảo hình vẽ).

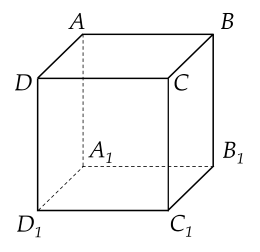
Góc giữa đường thẳng $AD$ và $BB_1$ bằng

Cho hình lập phương $ABCD.A'B'C'D'$.

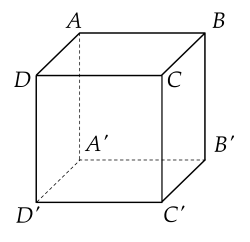
Đường thẳng $AC'$ vuông góc với mặt phẳng nào sau đây?

Cho hình chóp $S.ABCD$ có đáy là hình chữ nhật có $AB=2a\sqrt{3}$; $AD=2a.$ $H$ là trung điểm của $AB$, $SH=3a$ và vuông góc với đáy. $\tan$ góc giữa $SC$ và $\left(ABCD \right)$ bằng

Cho hình chóp $S.ABC$ có đáy là tam giác đều cạnh $2a$. Biết $SA=a\sqrt{3}$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Khoảng cách từ điểm $S$ đến đường thẳng $BC$ bằng

Cho hình chóp $S.ABC$ có $SA \bot \left(ABC \right)$, $\Delta ABC$ là tam giác đều cạnh $a$ và $SA=a\sqrt{3}$. Khoảng cách từ điểm $A$ đến mặt phẳng $\left(SBC \right)$ bằng

Cho hình chóp $S.ABCD$ có đáy là hình thoi cạnh $2a$, $\widehat{ADC}={{60}^{\circ}}$, $SA=6a$, $SA\bot \left(ABCD \right)$. Gọi $M$ là trung điểm của $SB$. Góc giữa hai đường thẳng $SA$ và $CM$ bằng