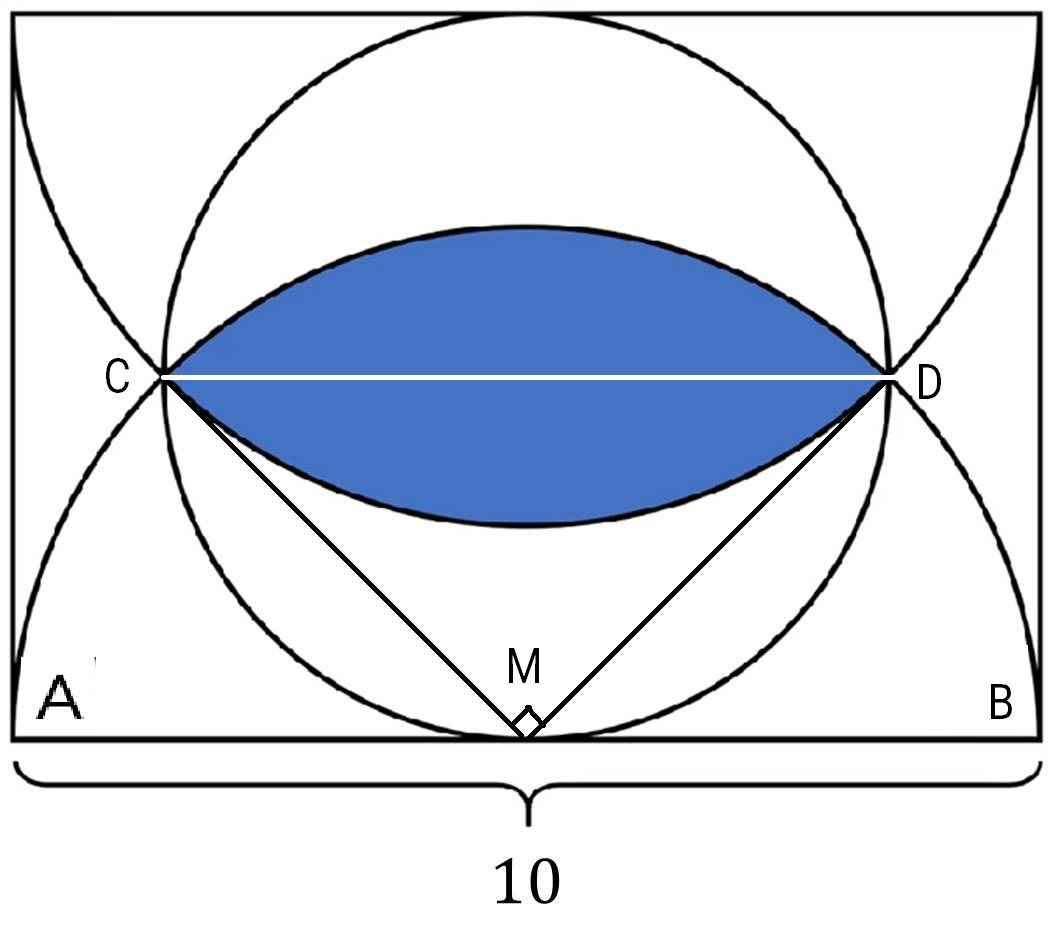
Ta có: MC = MD = MA =10/2 = 5(đvđd)(cùng là bán kính của đường tròn tâm M)

Vì ΔMCD nội tiếp hình tròn có tâm là trung điểm của CD nên \(\widehat{CMD}=90^O\)

Diện tích hình quạt tròn cung \(90^o\) giới hạn bởi MC và MD là: \(S=\dfrac{\pi R^2n}{360}=\dfrac{\pi\cdot5^2\cdot90}{360}=\dfrac{25\pi}{4}\left(đvdt\right)\)

Diện tích ΔMCD là: \(S_{MCD}=\dfrac{5\cdot5}{2}=\dfrac{25}{2}\left(dvdt\right)\)

Một nửa phần được tô màu có diện tích là: \(S_1=S-S_{MCD}=\dfrac{25}{4}\pi-\dfrac{25}{2}\left(đvdt\right)\)

Vậy diện tích phần được tô màu là: \(2S_1=\dfrac{25}{2}\pi-25\left(đvdt\right)\)